Apparate: Early-Exit Models for ML Latency and Throughput Optimization - Accurate Threshold Tuning

:::info Authors:

(1) Yinwei Dai, Princeton University (Equal contributions);

(2) Rui Pan, Princeton University (Equal contributions);

(3) Anand Iyer, Georgia Institute of Technology;

(4) Ravi Netravali, Georgia Institute of Technology.

:::

Abstract and 1 Introduction

2 Background and Motivation and 2.1 Model Serving Platforms

2.2 Early-Exit Models

2.3 Challenges

3 Design

3.1 Preparing Models with Early Exits

3.2 Accuracy-Aware Threshold Tuning

3.3 Latency-Focused Ramp Adjustments

4 Implementation

5 Evaluation and 5.1 Methodology

5.2 Overall Results

5.3 Comparison with Existing EE Strategies

5.4 Microbenchmarks

6 Additional Related Work

7 Conclusion, References, Appendix

To avoid accuracy drops as workload characteristics change over time, Apparate’s controller employs frequent and fast tuning of thresholds for already-enabled ramps. The reason is that threshold tuning for any set of ramps is sufficient to ensure that user-specified accuracy constraints are not violated – at the extreme, all thresholds could be set to zero, which precludes any early exiting. Altering only the set of active ramps fails to provide this property.

\ To enable threshold tuning, as requests pass through a model, Apparate’s controller continually records exiting information at each active ramp, as well as the final result that the original model predicts. More precisely, for each ramp, Apparate records the result (e.g., classification label) with the lowest error rate, i.e., the highest-confidence result for the ramp, even if the error exceeds the ramp’s threshold (precluding exiting). Importantly, since inputs always pass fully through models with Apparate, this information is recorded for all inputs at each active ramp, irrespective of upstream exiting decisions. This is paramount since the information

\

\ serves not only as a signal for when to tune thresholds, but also provides guidance for how to do so.

\ Triggering tuning. Apparate maintains an average achieved accuracy over the past 16 samples by comparing exiting results with the deployed configuration to results of the original model. Threshold tuning is triggered any time a window’s accuracy falls below the user-specified accuracy constraint. The threshold tuning process (described below) runs asynchronously on a CPU, without any disruptions to ongoing jobs. This is possible since thresholds are anyway enforced only by Apparate’s controller; GPUs are agnostic to threshold values, and instead simply stream ramp results to the Apparate controller which determines exiting decisions.

\ Evaluating threshold configurations. Threshold tuning requires insight into how any alterations to active ramp thresholds would affect overall model exiting behavior (and accuracies). The aforementioned per-request, per-ramp monitoring information grants this visibility, enabling Apparate to rapidly evaluate any threshold values across active ramps without requiring additional inference, and while accounting for inter-ramp dependencies. In particular, to evaluate new threshold values, Apparate simply identifies the earliest ramp whose top prediction now has an error rate below its threshold. Comparing these results with those of the original model indicates the achieved accuracy for the new configuration; latency wins for these exit patterns are computed using the one-time profiling data described in §3.3.

\

\

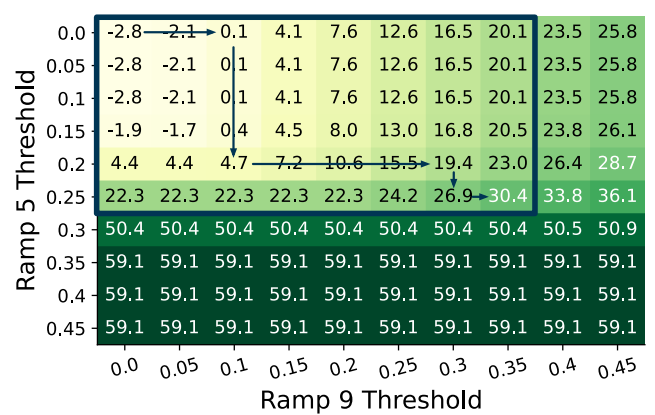
\ Instead, Apparate employs a greedy heuristic (Algorithm 1 in §A) that leverages a fundamental property of EEs when evaluated against an original model: higher thresholds result in monotonic decreases in accuracy and monotonic increases in latency savings. This prunes the space of threshold values to consider by providing a clear boundary in the Rdimensional space that separates configurations that are sufficiently accurate from those that are not. Additionally, for accurate configurations, maximum latency savings must fall on that boundary. Figure 10 illustrates this.

\ These properties inform Apparate’s hill climbing strategy [47] for threshold tuning. Starting with threshold values of 0 for each active ramp, and a step size of 0.1, threshold tuning runs in a series of (incremental) exploration rounds. In each round, we increase the threshold of each ramp in isolation (leaving the others unchanged), and evaluate the achieved accuracy and latency savings as described above. Apparate then chooses the single ramp threshold change that delivered the largest additional latency savings per unit of additional accuracy loss. This process repeats until no ramp’s threshold can be increased without an accuracy violation.

\ To enhance this process, Apparate follows a multiplicative increase, multiplicative decrease policy on step sizes to balance search speed and granularity. Specifically, each time a step increase results in an accuracy violation, Apparate halves that ramp’s step size for subsequent rounds to hone in on the boundary at fine granularity; step sizes are lower-bounded at 0.01. Conversely, selection of a ramp for threshold alteration suggests a potentially promising path of exploration; in this case, for a speedup, Apparate doubles that ramp’s step size for the following round.

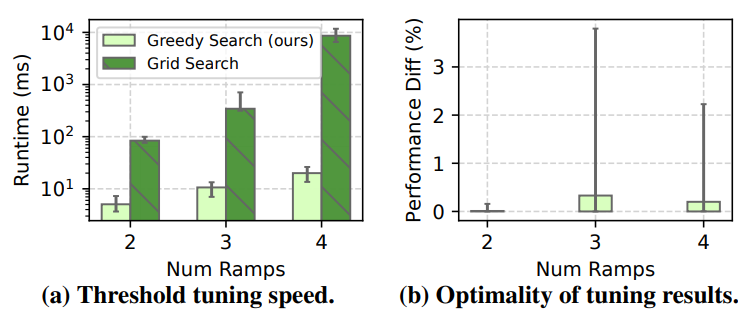
\ Overall, as shown in Figure 11, Apparate’s threshold tuning algorithm runs up to 3 orders of magnitude faster than a pure grid search (11.9ms vs. 3.0s on average). Note that these results maximally parallelize grid search across a 30-core machine. Further, selected threshold values achieve within 0-3.8% of the latency savings of the optimal configurations.

\

:::info This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.

:::

\