Quantum Critical Engine at Finite Temperatures: Transverse Ising Model as Working Medium

:::info Authors:

(1) Revathy B S, Raman Research Institute, Bengaluru, 560080, Karnataka, India and Corresponding author;

(2) Victor Mukherjee, Department of Physical Sciences, Indian Institute of Science Education and Research Berhampur, Berhampur, 760010, Odisha, India;

(3) Uma Divakaran, Department of Physics, Indian Institute of Technology Palakkad, Palakkad, 678623, Kerala, India.

:::

Abstract and 1 Introduction

2 Free fermionic model

3 Many body quantum Otto cycle

4 Universal scalings in work output

5 Transverse Ising model as working medium

6 Conclusion and References

We demonstrate the results derived in the previous section using the prototypical model of transverse Ising model (TIM) as the WM of the Otto cycle. The Hamiltonian of TIM is given by

\

\ When written in momentum (k) space using the basis |0, 0⟩, |k, 0⟩, |0, −k⟩, |k, −k⟩, the Hamiltonian takes the form

\

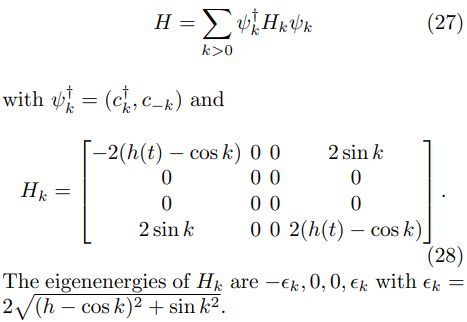
\ During the unitary strokes of the QOC, the transverse field is changed from h1 to h2 in the B → C stroke using the driving protocol

\

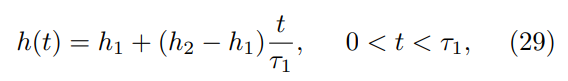
\ and vice versa in the D → A stroke using the protocol

\

\ For TIM, the value of the critical exponents are

\

\ ν = z = 1 which gives

\

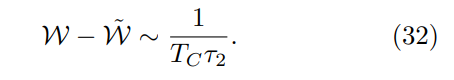
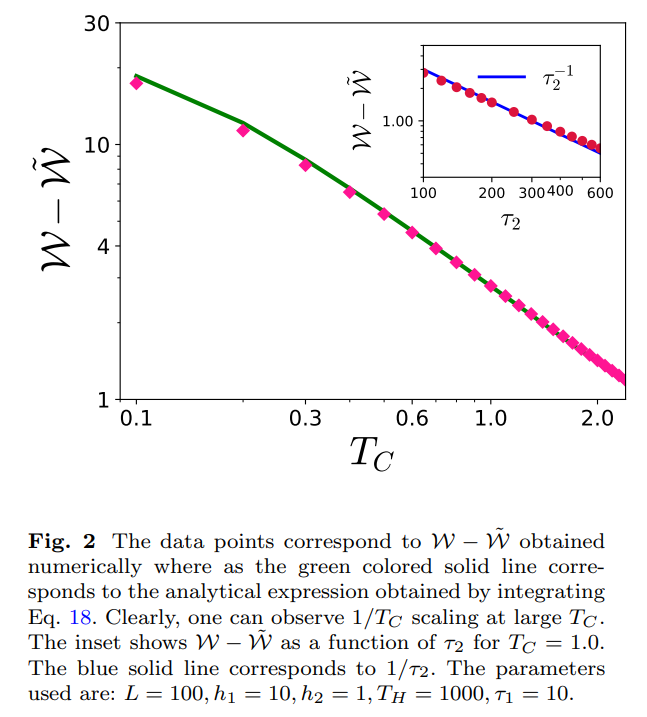
\ One can also obtain the expression for excess defects or excess energy by integrating the analytical expression given in Eq. 18 where pk is given by the Landau Zener probability which in our case takes the form

\

\

\

\

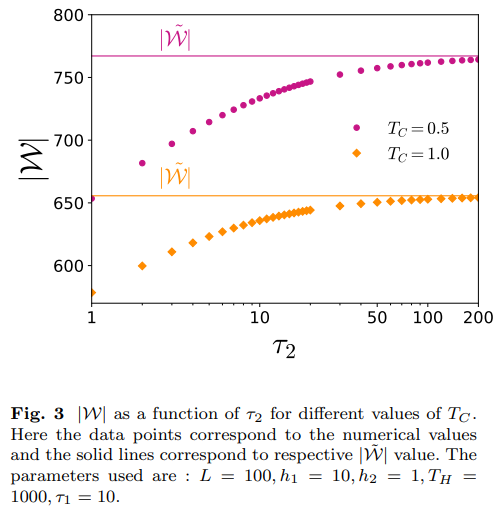
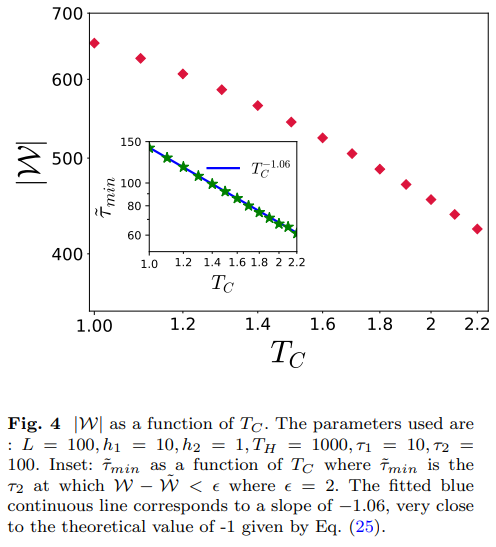
:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\