We consider a Bayesian persuasion problem where the sender tries to persuade the receiver to take a particular action via a sequence of signals. This we model by considering multi-phase trials with different experiments conducted based on the outcomes of prior experiments. In contrast to most of the literature, we consider the problem with constraints on signals imposed on the sender. This we achieve by fixing some of the experiments in an exogenous manner; these are called determined experiments. This modeling helps us understand real-world situations where this occurs: e.g., multi-phase drug trials where the FDA determines some of the experiments, start-up acquisition by big firms where the potential acquirer determines late-stage assessments, multi round job interviews where the candidates signal initially by presenting their qualifications but the rest of the screening procedures are determined by the interviewer. The non-determined experiments (signals) in the multi-phase trial are to be chosen by the sender to persuade the receiver best. With a binary state of the world, we derive the optimal signaling policy in the only non-trivial configuration of a two-phase trial with binary outcome experiments. We then generalize to multi-phase trials with binary-outcome experiments where the determined experiments can be placed at arbitrary nodes in the trial tree. Here we present a dynamic programming algorithm to derive the optimal signaling policy that uses the two-phase trial solution’s structural insights. We also contrast the optimal signaling policy structure with classical Bayesian persuasion strategies to highlight the impact of the signaling constraints on the sender.

\ Keywords: Information design · Bayesian persuasion · Signaling games.

1 Introduction

Information design studies how informed agents (senders) persuade uninformed agents (receivers) to take specific actions by influencing the uninformed agents’ beliefs via information disclosure in a game. The canonical Kamenica-Gentzkow model [16] is one where the sender can commit to an information disclosure policy (signaling strategy) before learning the true state. Once the state is realized, a corresponding (randomized) signal is sent to the receiver. Then, the receiver takes an action, which results in payoffs for both the sender and the receiver. Senders in information design problems only need to manipulate the receivers’ beliefs with properly chosen signals. The manipulated beliefs will create the right incentives for the receiver to spontaneously take specific actions that benefit the sender (in expectation). In (classical) mechanism design, however, the story is different: the designer is unaware of the agents’ private information, and the agents communicate their private information to the designer, who then has to provide incentives via (monetary) transfers or other means. The flexibility afforded by information design that allows the sender to benefit from information disclosure without implementing utility-transfer mechanisms has led to greater applicability of the methodology: various models and theories can be found in survey papers such as [3] and [15].

\ Our work is motivated by many real-world problems where persuasion schemes are applicable, but the sender is constrained in the choice of signals available for information design. Specifically, we are interested in problems that are naturally modeled via multi-phase trials where the interim outcomes determine the subsequent experiments. Further, we insist that some of the experiments are given in an exogenous manner. This feature imposes restrictions on the sender’s signaling space, and without it, we would have a classical Bayesian persuasion problem with an enlarged signal space. Our goal is to study the impact of such constraints on the optimal signaling scheme, and in particular, to contrast it with the optimal signaling schemes in classical Bayesian persuasion.

\ The following motivating example describes a possible real-world scenario.

\ Example 1 (Motivating example - Acquiring funds from a venture capital firm). We consider a scenario where a start-up is seeking funds from a venture capital firm. The process for this will typically involve multiple rounds of negotiation and evaluation: some of these will be demonstrations of the start-up’s core business idea, and the others will be assessments by the venture capital firm following their own screening procedures. The start-up will have to follow the venture capital firm’s screening procedures but chooses its product demonstrations. Based on these stipulations, the start-up needs to design its demonstrations to maximize its chance of getting funded.

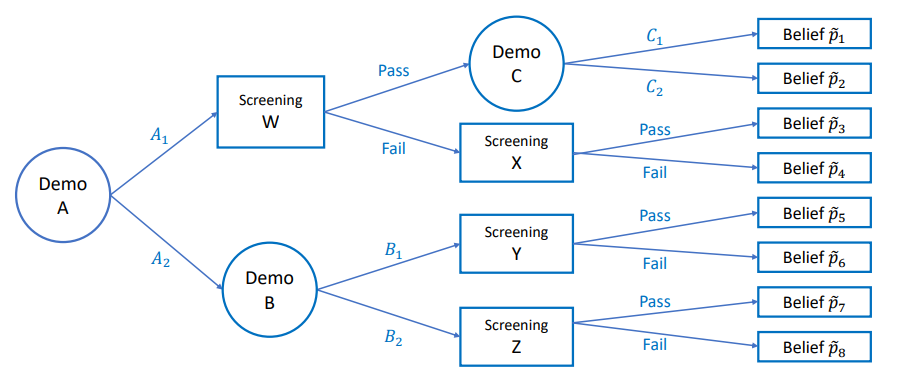
\ Fig. 1. Example of a negotiation process – a startup vs. a venture capital firm.

\ In the example above, the start-up (sender) has to generate an information disclosure scheme to get the desired funds from the venture capital firm (receiver). Then the screening procedures set by the venture capital firm are analogous to our determined experiments, and the demonstrations carried out by the start-up are the (sender) designed experiments. For example, in Figure 1 we present one plausible interaction where the start-up company designs demonstrations A, B, and C (circles in the figure) and the venture capital firm has pre-determined screening examinations W, X, Y, and Z (rectangles in the figure). Whereas we have illustrated this example via a balanced tree, if we have an unbalanced tree owing to the receiver deciding in the middle, we can modify it to a balanced tree by adding the required number of dummy stages.

\ The sender’s reduced flexibility on her signaling strategies under some predetermined experiments with arbitrary positions and informativeness differentiates our work from the growing literature on dynamic information design. Our model considers a problem with the following features: a static state space, a sequential information disclosure environment, and a signaling space restricted by some exogenous constraints whose harshness may depend on the proposed singling schemes. Models with a static state space, an unrestricted signal space but a variety of sequential information disclosure environments have been studied to capture features in different real-world problems: e.g., with multiple senders [12,19], with costly communication [14,22], allowing for sequential decision making [10], or with partial commitment [1,22]. Models with dynamic states and sequential information disclosure environments are usually studied under an informed sender with the knowledge of dynamically changing state(s); a variety of works in this category lie in state change detection [9,11] or routing games [21]. Although several works [7,13,18] also consider constrained signaling schemes, these works either consider the signal space to be smaller than the action space [13,7] or consider a noisy signaling environment [18]. Models with exogenous information [17,5,4], can be viewed as sequential information disclosure problems with exogenous determined experiments placed in determined phases. The sequential information disclosure in our model, which actually enlarges the signal space, makes our work different from above works. To keep the focus of the paper on sequential trials, we discuss the broader literature on constrained senders, algorithmic information design, and works related to the receiver’s experiment design[1] in our online version [23].

\ According to the motivating example illustrated in Figure 1, the persuasion problem considers a sequence of experiments where experiments further along in the tree depend on the outcomes of previous phases. The experiment to be run in each phase is either exogenously determined or chosen by the sender. In the game, the sender chooses designed experiments with knowledge of the prior, the determined experiments, and the receiver’s utility function, but before the state of the world is realized. After the sender commits to the experiments (i.e., the signaling strategy), the state of the world is realized, and a specific sequence of experiments is conducted based on the realization of the underlying random variables. The receiver then takes an action depending on the entire sequence of outcomes. The prior, the sender’s and receiver’s utility functions, the determined experiments, and the designed experiments (after the sender finalizes them) are assumed to be common knowledge. We study this problem for binary states of the world, first for two-phase binary-outcome trials, and then generalized to multiphase binary-outcome trials. We then generalize to non-binary experiments (still with an underlying binary state space). In the online version [23] we add games with an additional stage where the receiver moves before the sender to decide some or all of the determined experiments, perhaps with some constraints.

\ Contributions: The main contributions of this work are:

To the best of our knowledge, within the multi-phase Bayesian persuasion framework, we are the first to study the design of sender’s signaling schemes with exogeneously determined experiments in arbitrary positions. Our results highlight the difference between “exogenously determined experiments” and “exogenously given information” in the dynamic information design, where the former gives greater flexibility and allows for more heterogeneity.

\
We explicitly solve the optimal signaling scheme in two-phase trials. Moreover, using structural insights gained from two-phase trials, we present a dynamic programming algorithm to derive the optimal signaling in general multi-phase trials via backward iteration.

\
We analyze the impact of constraints on the sender via the determined experiments by contrasting the performance with the classical Bayesian persuasion setting and when using classical Bayesian persuasion optimal signaling schemes when the sender is constrained. As a part of this, we provide a sufficient condition for when a sequential trial is equivalent to classical Bayesian persuasion with a potentially enlarged signal space.

:::info This paper is available on arxiv under CC 4.0 license.

:::

[1] See Section 5 in [23] for details.

Feed: Hacker Noon - Medium

View: Original article

Tags: framework underlying

Frameworks