and the distribution of digital products.
DM Television
A Historical Mathematical Concept Powers Information Retrieval In the Modern Age
In the world of information retrieval (IR), the need to quickly and accurately find relevant documents or data within vast repositories is crucial. With exponential growth in the volume of unstructured data—such as text, social media posts, images, and videos—search technologies face unprecedented challenges. Traditional keyword-based methods are often insufficient to surface the most relevant documents for a user query, especially as more complex semantics and context come into play.
\ This is where the vector space model and in particular, cosine similarity shine. These fundamental concepts provide the mathematical backbone for modern search techniques, including web search engines, recommendation systems, and advanced retrieval frameworks. By representing documents and queries as vectors, the problem of “finding the best match” can be boiled down to measuring similarity between vectors in a high-dimensional space. Cosine similarity, in particular, has become a workhorse due to its robustness and simplicity.
\ This article will explore briefly the mathematics (it may look scary initially, but its pretty basic and doesn’t need any advanced concepts) of how the vector space model and TF-IDF (Term Frequency–Inverse Document Frequency) weighting scheme work, discuss the foundations of cosine similarity (with an example), explore its critical applications in search, and consider the challenges and potential solutions for implementing cosine similarity at scale. We also provide some relevant references to landmark research in this domain.
What Is the Vector Space Model and TF-IDF? Defining the Vector Space ModelThe vector space model is a foundational concept in information retrieval introduced by Gerard Salton and his colleagues in the 1970s[1]. It represents text documents (and queries) as points—or vectors—in a multi-dimensional space, where each dimension corresponds to a distinct term (or feature). The central idea is that the similarity (or distance) between two vectors can be measured using standard mathematical approaches, such as the dot product, Euclidean distance, or cosine similarity. This model underlies many modern search engines and text analytics applications.
\
Document Representation: Suppose you have a vocabulary ***V = {w1, w2, w3,…, wn} ***comprising all unique words found in a corpus of documents. Each document d can be represented as a vector, where w is the weight of term w in document d. This weight can be determined in various ways, the most common being the TF-IDF scheme (explained later).
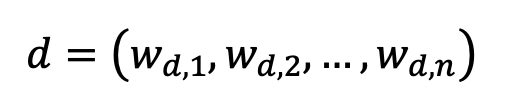
Query Representation: A user query can similarly be treated as a “very short document,” enabling direct comparison of documents and query in the same vector space.
\ By transforming documents (and queries) into numerical vectors, the problem of document retrieval becomes a matter of ranking documents by measuring their vector similarity to the query vector. One of the most effective similarity measures is cosine similarity, which we will discuss at length later.
Understanding TF-IDFThe Term Frequency–Inverse Document Frequency (TF-IDF) weighting scheme is a cornerstone of text analysis and search. It aims to quantify the importance of each term in a document (relative to the entire corpus). TF-IDF is calculated in two steps:
\
Term Frequency (TF): TF(t, d) measures how frequently term t occurs in document d. A simple approach is as shown below. This captures the idea that the more frequently a term appears in a document, the more important it is to that document’s meaning.
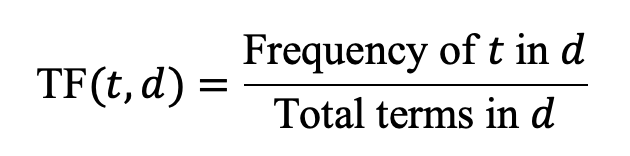
Inverse Document Frequency (IDF): IDF (t, D) measures how informative a term t is across the entire collection of documents D. It is inversely proportional to the number of documents in which the term appears as shown below. Terms that occur in many documents (e.g., stop words like “the,” “is,” or “and”) will have a low IDF, while rare terms will have a higher IDF.
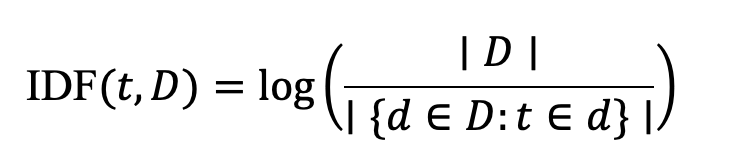
Putting these together, the TF-IDF weight of a term t in document d is:
\ TF-IDF (t, d) = TF (t, d) x IDF (t, D)
\ **Short Example \ Imagine a small corpus of three documents:
1. d1: “the cat sat on the mat”
2. d2: “the dog chased the cat”
3. d3: “the mouse ran away”
\ Let’s consider the TF-IDF of the term “cat” in these three documents.
\
Term Frequency of “cat” in d1 is 1/6 (since “cat” appears once among six total words). In d2, TF is 1/5. In d3, TF is 0 because “cat” does not appear.
Inverse Document Frequency for “cat,” assuming the logarithmic formula (the term “cat” appears in 2 of the 3 documents):
**IDF (cat, D) = log(3/2) = 0.405 (approx)**
\ Therefore, we can calculate now the TF-IDF for word “cat” in each document-
- TF-IDF (cat, d1) = (1/6) x 0.405 = 0.0675 (approx)
- TF-IDF (cat, d2) = (1/5) x 0.405 = 0.081 (approx)
- TF-IDF (cat, d3) = 0
\ These TF-IDF values for each term t (e.g. cat) would form part of the vector representation of each document. Next, we would measure how similar these vectors are to a query (like “cat mat”) to rank documents for relevance.
What Is Cosine Similarity?Cosine similarity is a measure of similarity between two vectors that calculates the cosine of the angle between them. Given two vectors A and B, their cosine similarity is:
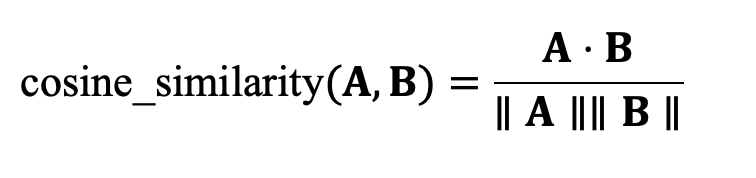
where:
- A . B is the dot product of vectors A and B.
- || A || and || B || are the Euclidean (L2) norms of the respective vectors.
\ Cosine similarity ranges from -1 (exactly opposite) to 1 (exactly the same), with 0 indicating orthogonality (i.e., no similarity). In text analysis, because TF-IDF weights are typically non-negative, the range is usually [0, 1], where 0 means no shared terms and 1 means identical term distributions.
\
Example CalculationConsider two TF-IDF vectors, A and B, each with TF-IDF values corresponding to terms {t1, t2, t3}. Suppose:
\ A = (0.1, 0.3, 0.5), B = (0.2, 0.3, 0)
\
Dot Product:
A . B = (0.1 x 0.2) + (0.3 x 0.3) + (0.5 x 0) = 0.02 + 0.09 + 0 = 0.11
\
Norms:
|| A || = Sqrt((0.1)^2 + (0.3)^2 + (0.5)^2) = 0.5916 (approx)
|| B || = Sqrt((0.2)^2 + (0.3)^2 + (0)^2) = 0.3606 (approx)
\
Cosine Similarity:
cosine_similarity (A, B) = 0.11 / (0.5916 x 0.3606) = 0.5157 (approx)
\ A similarity of approximately 0.52 implies a moderate overlap in terms between these two vectors. In a real-world search scenario, you would compute this measure for each document relative to the query vector to rank documents by relevance.
\
Applications of Cosine SimilarityThe versatility of cosine similarity extends well beyond simple text matching. Below are some key areas where cosine similarity has become an essential technique.
\
Web Search Engines
Relevance Ranking: Major search engines (like Google and Bing) incorporate variants of the vector space model, often weighting terms via TF-IDF-like measures or advanced distributional representations. Cosine similarity (or more advanced similarity measures) is used to identify how closely a document aligns with a user’s query.
Ad Retrieval Systems: Online advertising platforms often rely on semantic matching techniques (where the meaning of the query or webpage is used to retrieve relevant ads). Cosine similarity is fundamental to these matching algorithms.
\
Recommendation Systems
Content-Based Recommendations: Systems that recommend content (e.g., news articles, blog posts, YouTube videos) often compute TF-IDF vectors of items and then rank them by cosine similarity to a user’s preference profile.
Item-Item or User-User Similarity: In collaborative filtering, user preferences can be turned into vectors, and cosine similarity helps cluster like-minded users or items with similar traits.
\
Document Clustering and Classification
Clustering: Algorithms such as k-means or hierarchical clustering often rely on distance or similarity metrics. Since cosine similarity is invariant to the magnitude of vectors, it is especially useful in text clustering where vector magnitudes can be heavily influenced by document lengths.
Classification: In text classification tasks (like spam filtering), classifiers (e.g., nearest neighbor methods) measure similarity between an incoming document and known classes. Cosine similarity is a common choice for these comparisons.
\
Semantic Textual Analysis
Topic Modeling: Techniques like Latent Dirichlet Allocation (LDA) produce topic distributions for documents. Cosine similarity can then be used to measure how similar two documents are in terms of their topic distributions.
Word Embeddings: Word embeddings (e.g., Word2Vec, GloVe) map words to dense vectors in a continuous vector space. Cosine similarity is widely used to measure semantic similarity between words (or phrases).
\
Natural Language Processing
Sentence or Paragraph Similarity: In tasks such as paraphrase detection, summarization, or semantic textual similarity, each text segment is converted into a vector (using TF-IDF, BERT embeddings, etc.). Cosine similarity is then used to determine how closely the meanings align.
Entity Linking: When linking mentions of entities in text to knowledge bases (like Wikipedia), similarity measures determine the best match among multiple candidates.
While cosine similarity is a powerful and widely used metric, it is not without its challenges. Below are some considerations to ensure optimal performance and maintainability in real-world applications.
\
High-Dimensional Sparse Vectors
Challenge: In large document collections, you might have tens or hundreds of thousands of unique terms. This leads to very high-dimensional vectors, most of which are sparse (i.e., contain many zeros).
Potential Solution: Use sparse data structures and efficient libraries (e.g., SciPy in Python) that can handle sparse vector arithmetic. Dimensionality reduction techniques (e.g., PCA, SVD, autoencoders) can also help manage high-dimensional data.
\
Vocabulary Size and Stop Words
Challenge: Common words (like stop words) can overwhelm more meaningful terms if not properly handled. Also, synonyms and morphological variations increase vocabulary size unnecessarily.
Potential Solutions:
Apply stop word removal to reduce noise.
Use stemming or lemmatization to handle morphological variations.
Consider domain-specific vocabularies or controlled taxonomies for specialized applications.
\
Weighting Schemes
Challenge: Plain TF-IDF may not always capture complex linguistic phenomena, such as context or polysemy. Additionally, frequent updates to your corpus can change IDF values frequently.
Potential Solutions:
Explore advanced methods like BM25 (a popular ranking function in IR that extends TF-IDF), or neural-based embeddings (e.g., BERT, GPT-style embeddings).
Maintain a dynamic pipeline to re-calculate IDF values periodically if your document set changes significantly.
\
Scale and Real-Time Applications
Challenge: Storing and computing similarity for millions (or billions) of documents in real time is computationally expensive.
Potential Solutions:
Employ inverted indexes (common in search engines) to quickly retrieve candidate documents that share terms with a query.
Precompute indexes of term vectors using specialized IR frameworks like Elasticsearch or Apache Lucene, which internally optimize cosine or BM25-like similarity.
Use approximate nearest neighbor search techniques (e.g., FAISS, Annoy, or HNSW) for vector embeddings to reduce retrieval times in large-scale systems.
\
Interpretability vs. Black-Box Models
Challenge: As more advanced (e.g., transformer-based) embeddings become prevalent, the interpretability of similarity scores can diminish.
Potential Solutions:
Provide additional context or metadata in your search results to justify matches.
Hybrid models that combine classic TF-IDF-based approaches with neural embeddings can balance interpretability (from TF-IDF) and nuanced semantic understanding (from deep embeddings).
\
Domain-Specific Customizations
Challenge: Different domains (e.g., legal, medical, scientific) use specialized terminology, meaning a generic approach might miss domain nuances.
Potential Solutions:
Build domain-specific dictionaries or vocabularies.
Fine-tune pre-trained models (e.g., BERT) on domain corpora.
Continually evaluate retrieval quality using domain-specific metrics.
\
Cosine similarity underpins countless applications in modern information retrieval and natural language processing. By representing both queries and documents as vectors—often weighted via TF-IDF—search systems can rank relevance by simple yet effective geometric measures. Cosine similarity’s strength lies in its interpretability, computational efficiency, and alignment with the intuitive concept of matching overlapping features between documents.
\ However, implementing cosine similarity in production requires careful attention to data structures, vocabulary management, and the inherent trade-offs of scale and domain specificity. As the industry moves toward neural embeddings and large language models, cosine similarity remains an essential building block. Even in deep learning pipelines, the final step of matching or ranking often relies on a similarity measure like cosine to determine how closely representations match.
\ For organizations and researchers looking to improve or build search functionalities, understanding fundamentals like vector space model, TF-IDF, and cosine similarity is important. With appropriate optimizations, these methods can scale to massive document collections while providing interpretable and robust relevance measures. Through hybrid models and advanced embeddings, the role of cosine similarity only grows more prominent, enabling increasingly sophisticated and accurate search experiences.
ReferencesBelow are some landmark research papers and books in the field of information retrieval and text similarity, along with practical resources for implementation:
\
Salton, G., Wong, A., & Yang, C. S. (1975). A Vector Space Model for Automatic Indexing. Communications of the ACM, 18(11), 613–620.
This seminal paper introduced the Vector Space Model, laying the groundwork for modern text retrieval systems.
Salton, G. & Buckley, C. (1988). Term-weighting approaches in automatic text retrieval. Information Processing & Management, 24(5), 513–523.
A classic reference for understanding TF-IDF and other weighting schemes.
Manning, C. D., Raghavan, P., & Schütze, H. (2008). Introduction to Information Retrieval. Cambridge University Press.
A comprehensive textbook covering classical IR, including TF-IDF, vector space models, and cosine similarity.
Baeza-Yates, R., & Ribeiro-Neto, B. (2011). Modern Information Retrieval: The Concepts and Technology behind Search (2nd ed.). Addison-Wesley.
An authoritative resource on the architecture and algorithms powering modern search engines.
Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer, T. K., & Harshman, R. (1990). Indexing by Latent Semantic Analysis. Journal of the American Society for Information Science, 41(6), 391–407.
Introduced Latent Semantic Analysis (LSA), a precursor to modern vector-based models for text.
BERT: Devlin, J., Chang, M. W., Lee, K., & Toutanova, K. (2019). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. NAACL-HLT.
Although not directly about cosine similarity, BERT-based embeddings frequently use cosine similarity for downstream tasks like sentence and document similarity.
Elasticsearch and Lucene Documentation
Official guides to popular open-source search engines that internally use variations of TF-IDF and cosine similarity for ranking.
FAISS (Facebook AI Similarity Search): https://github.com/facebookresearch/faiss
An open-source library for efficient similarity search and clustering of dense vectors.
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright 2025, Central Coast Communications, Inc.