and the distribution of digital products.
Evaluating Deep RL Agents in Hedging with Market-Calibrated Stochastic Volatility Models
Introduction
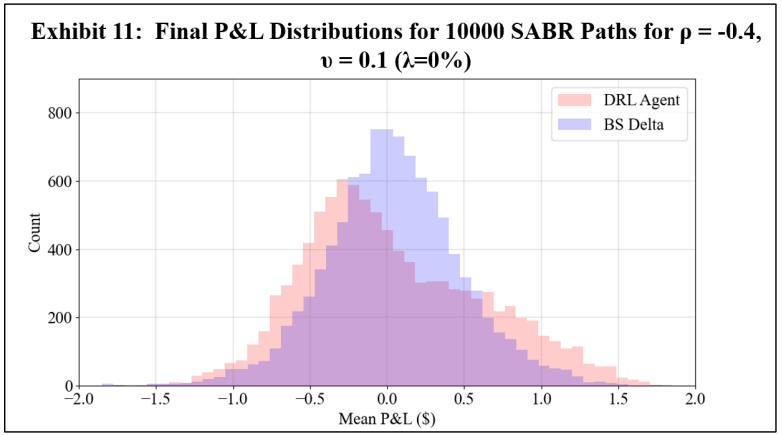
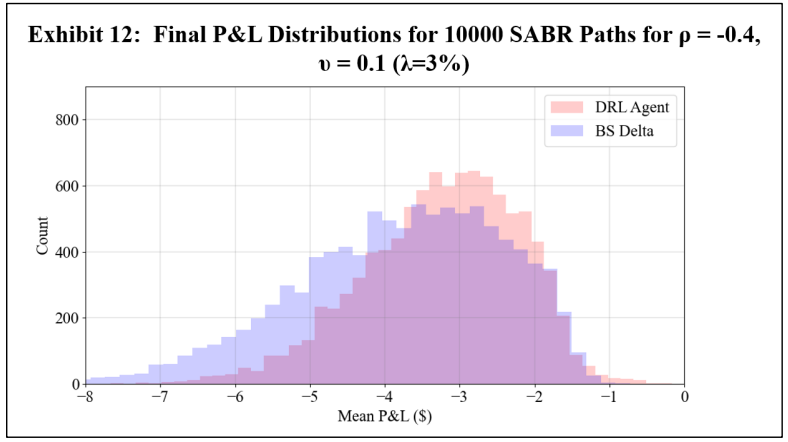
To assess a real-world application of DRL hedging, agents are trained using marketcalibrated stochastic volatility model paths. Recall however that to establish a baseline, a first experiment uses arbitrary model coefficients. For this initial experiment, Exhibits 11 and 12 show the final P&L distributions of the DRL and BS Delta strategies under 0% and 3% transaction costs, respectively, and Exhibit 13 shows the summary statistics of both cases.
\
\
\
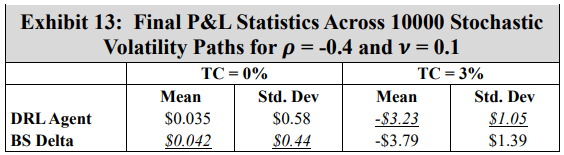
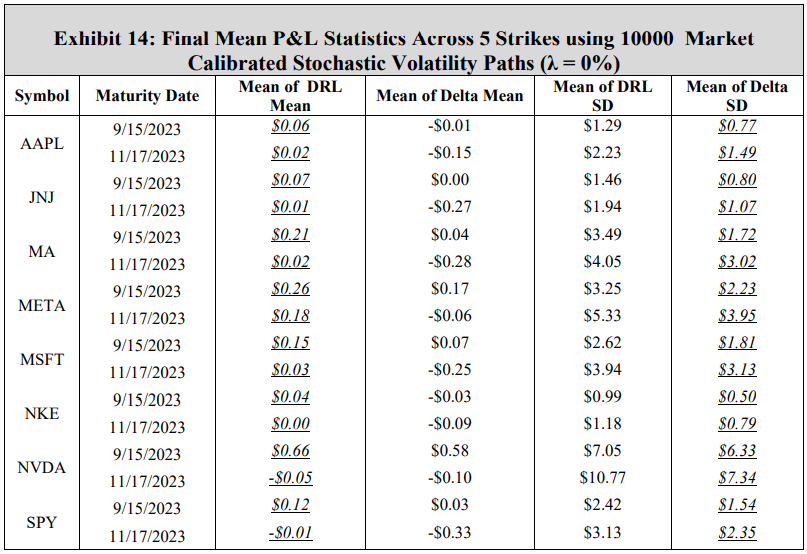
\ The results are consistent with the GBM experiments, showing that under transaction costs, the DRL agent outperforms the BS Delta strategy, producing a higher mean final P&L and a lower standard deviation. The real-world application may now be examined using the DRL agents trained with market calibrated models. To present results without listing all 80 options, the mean and standard deviation of mean final P&L result across five strikes for each symbol and maturity date is computed. These final P&L statistics for both the DRL agent and the BS Delta strategy are summarized in Exhibit 14 for a transaction cost-free scenario, and in Exhibit 15 for a 3% transaction costs. The reader should not compare results between different rows, as the results are functions of both symbol prices and maturities. The DRL and BS Delta final P&Ls statistics for all 80 options are listed in the Appendix.
\
\
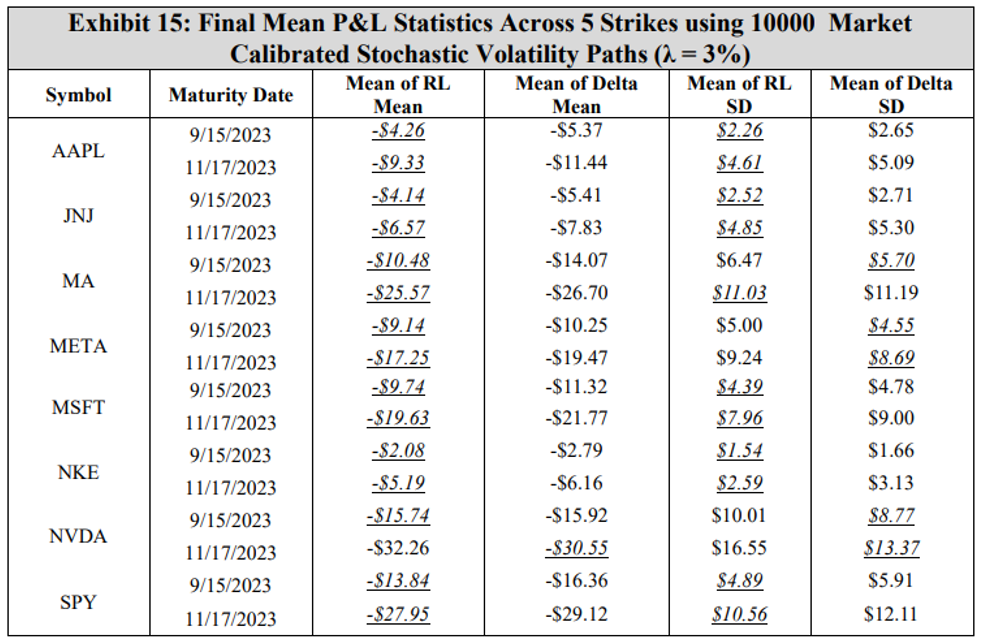
\ When there are no transaction costs, both the DRL agent and the BS Delta strategy achieve near-zero means in all cases, indicating effective hedging performance. These results show that the DRL strategy achieves a higher mean final P&L in all 16 cases, while the BS Delta strategy yields a lower standard deviation in all cases. With a 3% transaction cost rate, the results indicate that the DRL agent achieves a higher mean of mean final P&Ls across the five strikes than the BS Delta strategy in all but one symbol and maturity date combinations (NVDA 11/17/2023). Moreover, the DRL agent achieves a lower mean standard deviation in 11 of 16 cases, exemplifying that the DRL agents hedge in a consistent manner that achieves a lower variance on average than a BS Delta strategy. This outcome implies that when transaction costs are incorporated, training a DRL agent with calibrated stochastic volatility model parameters is more effective than computing a BS Delta hedge using the model-derived volatility at each time step.
\ Now, the DRL agent is tested on the empirical asset price data between the sale and maturity dates. Note that as the experiment aims to assess only the performance of the DRL agent in a realistic scenario, only an environment with a 3% transaction cost rate is used for testing. Exhibit 16 summarizes the mean final P&L for both the DRL agent and the BS Delta strategy across the five strikes for each symbol and maturity. Again, results should not be compared across rows, as the results are a function of both the underlying asset price process and the maturity date. The final hedging P&L for all 80 options using the true asset paths are listed in the Appendix.
\
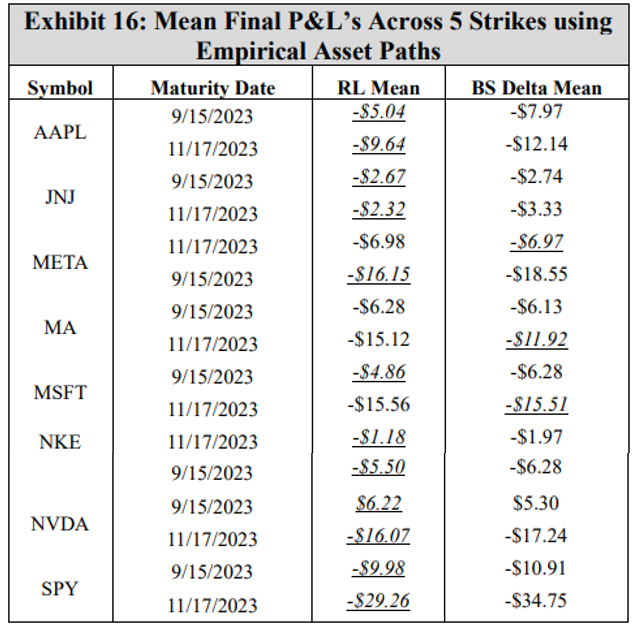
\ Using the actual asset paths for testing, the DRL agent outperforms the BS Delta strategy across the five strikes in 12 of 16 instances. As such, this outcome shows that not only do DRL agents achieve strong performance under simulated asset paths, maintaining consistency with the stochastic volatility model employed during training, but DRL agents also possess a desirable robustness in effectively hedging against empirical stock price movements. This is an important result, as it shows that on any given day, observed option prices may be used to train a DRL agent capable of hedging said option. Consider, for example, a trader with a basket of 80 options: the results from this work suggest that this trader can train a DRL agent for each option and achieve better performance than a BS Delta strategy. As such, a worthwhile future direction for this research would be to train the DRL agents anew on each day given the observed option prices. Further, as DRL becomes more prevalent in the hedging space, a worthwhile next step could be a parametric study that evaluates the impacts of various training hyperparameters such as the learning rates, episodes, re-balance steps, batch sizes, and reward functions. As there is currently no consensus in the DRL hedging literature towards hyperparameters and training best practices, this future study would help provide key information for practitioners attempting to employ their own DRL agents.
\
:::info Authors:
(1) Reilly Pickard, Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON M5S 3G8, Canada ([email protected]);
(2) Finn Wredenhagen, Ernst & Young LLP, Toronto, ON, M5H 0B3, Canada;
(3) Julio DeJesus, Ernst & Young LLP, Toronto, ON, M5H 0B3, Canada;
(4) Mario Schlener, Ernst & Young LLP, Toronto, ON, M5H 0B3, Canada;
(5) Yuri Lawryshyn, Department of Chemical Engineering and Applied Chemistry, University of Toronto, Toronto, ON M5S 3E5, Canada.
:::
:::info This paper is available on arxiv under CC BY-NC-SA 4.0 Deed (Attribution-Noncommercial-Sharelike 4.0 International) license.
:::
\