What Eigenvalue Conditions Mean for Economic Models

:::info Author:

(1) David Staines.

:::

Table of Links

Abstract

1 Introduction

2 Mathematical Arguments

3 Outline and Preview

4 Calvo Framework and 4.1 Household’s Problem

4.2 Preferences

4.3 Household Equilibrium Conditions

4.4 Price-Setting Problem

4.5 Nominal Equilibrium Conditions

4.6 Real Equilibrium Conditions and 4.7 Shocks

4.8 Recursive Equilibrium

5 Existing Solutions

5.1 Singular Phillips Curve

5.2 Persistence and Policy Puzzles

5.3 Two Comparison Models

5.4 Lucas Critique

6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems

6.2 Equilibrium Construction

6.3 Literature Comparison

6.4 Equilibrium Analysis

7 General Linearized Phillips Curve

7.1 Slope Coefficients

7.2 Error Coefficients

8 Existence Results and 8.1 Main Results

8.2 Key Proofs

8.3 Discussion

9 Bifurcation Analysis

9.1 Analytic Aspects

9.2 Algebraic Aspects (I) Singularities and Covers

9.3 Algebraic Aspects (II) Homology

9.4 Algebraic Aspects (III) Schemes

9.5 Wider Economic Interpretations

10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs

10.2 Econometric Duality

10.3 Coefficient Properties

10.4 Microeconomic Interpretation

11 Policy Rule

12 Conclusions and References

\ Appendices

A Proof of Theorem 2 and A.1 Proof of Part (i)

A.2 Behaviour of ∆

A.3 Proof Part (iii)

B Proofs from Section 4 and B.1 Individual Product Demand (4.2)

B.2 Flexible Price Equilibrium and ZINSS (4.4)

B.3 Price Dispersion (4.5)

B.4 Cost Minimization (4.6) and (10.4)

B.5 Consolidation (4.8)

C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence

C.2 Extending No Persistence

D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium

D.2 Profits and Long-Run Growth

E Slopes and Eigenvalues and E.1 Slope Coefficients

E.2 Linearized DSGE Solution

E.3 Eigenvalue Conditions

E.4 Rouche’s Theorem Conditions

F Abstract Algebra and F.1 Homology Groups

F.2 Basic Categories

F.3 De Rham Cohomology

F.4 Marginal Costs and Inflation

G Further Keynesian Models and G.1 Taylor Pricing

G.2 Calvo Wage Phillips Curve

G.3 Unconventional Policy Settings

H Empirical Robustness and H.1 Parameter Selection

H.2 Phillips Curve

I Additional Evidence and I.1 Other Structural Parameters

I.2 Lucas Critique

I.3 Trend Inflation Volatility

E.3 Eigenvalue Conditions

This last part contains derivations of the two eigenvalue polynomials in the text, starting with the simplest limiting case and moving onto the general.

\ E.3.1 √ ε Characteristic Equation

\ Abstracting from the errors, the system can be written as follows

\

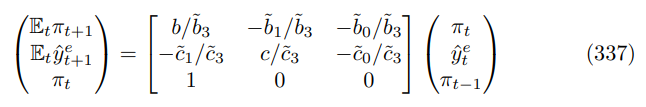
\ The characteristic polynomial comes from the following determinant equation

\

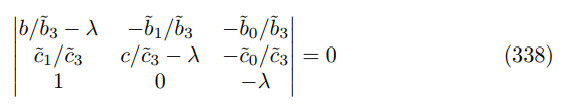
\ expressing in terms of minors gives

\

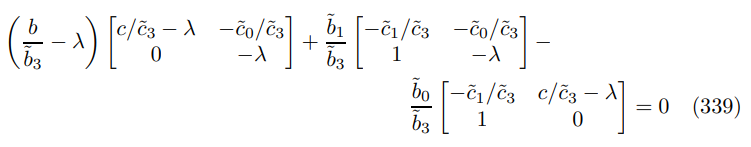
\ expanding out yields

\

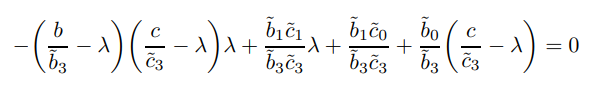
\ then a simple rearrangement gives the expression in the text.

\ E.3.2 General Characteristic Equation

\ Start from the characteristic matrix

\

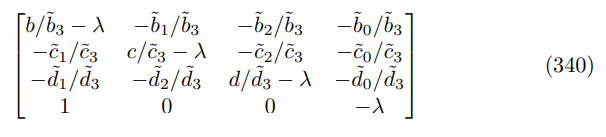
\ where I have reordered the variables (ˆπt, yˆt, ∆ˆ t, πˆt−1) ′ for convenience, substitution yields

\

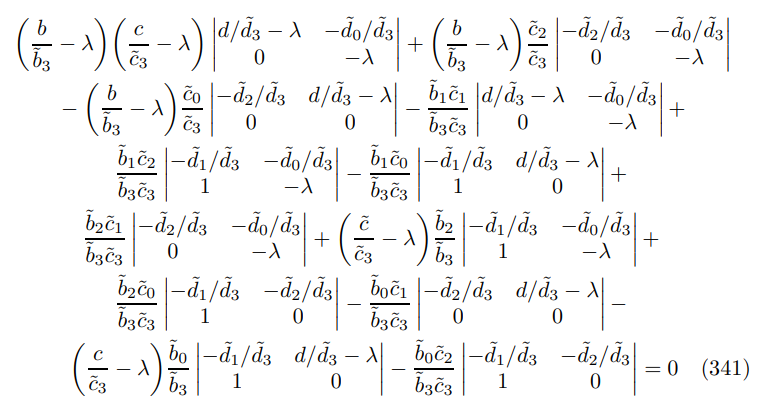
\ expanding out the matrices gives

\

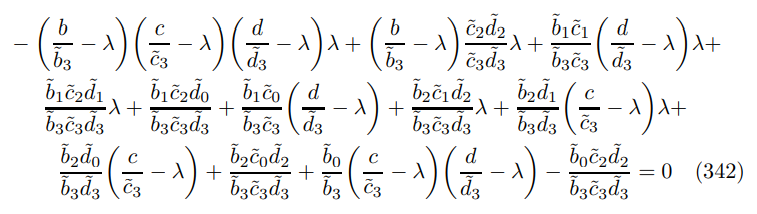
\ collecting terms implies the polynomial

\

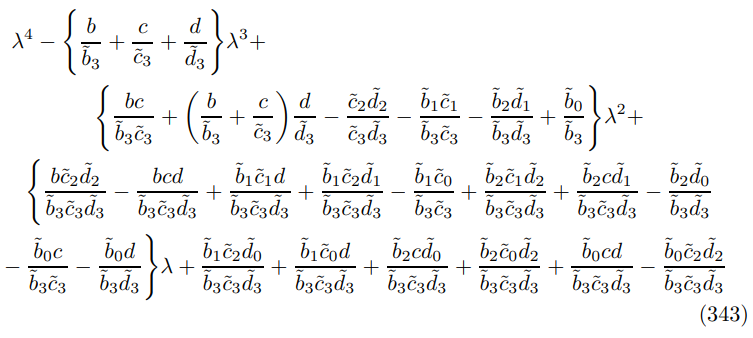
\ where perhaps the most challenging step is the expansion

\

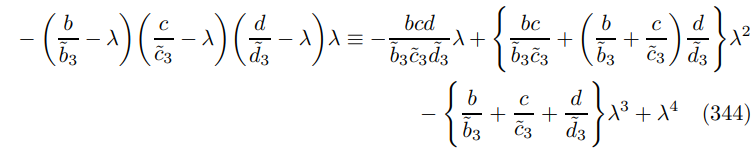
\ substituting in the ZINSS vanishing condition (138) yields the expression in Theorem 9.

\

:::info This paper is available on arxiv under CC 4.0 license.

:::

\