Two Algorithms, One Goal: Changing the Face of Anomaly Detection with KIF and SIF

:::info Authors:

(1) Guillaume Staerman, INRIA, CEA, Univ. Paris-Saclay, France;

(2) Marta Campi, CERIAH, Institut de l’Audition, Institut Pasteur, France;

(3) Gareth W. Peters, Department of Statistics & Applied Probability, University of California Santa Barbara, USA.

:::

Abstract and 1. Introduction

2. Background & Preliminaries

2.1. Functional Isolation Forest

2.2. The Signature Method

3. Signature Isolation Forest Method

4. Numerical Experiments

4.1. Parameters Sensitivity Analysis

4.2. Advantages of (K-)SIF over FIF

4.3. Real-data Anomaly Detection Benchmark

5. Discussion & Conclusion, Impact Statements, and References

\ Appendix

A. Additional Information About the Signature

B. K-SIF and SIF Algorithms

C. Additional Numerical Experiments

This section provides the algorithms for the two proposed methods, Kernel Signature Isolation Forest and Signature Isolation Forest. The steps for each algorithm are described and presented below, introducing the input of each procedure and the steps followed to construct the nodes of the partition trees and the children subsets and datasets. Finally, the output of each method is given. The details of these procedures are provided in the main paper in Section 3. Note that the ω parameter, corresponding to the number of split windows used for the signature, is considered as input since it must be chosen for the procedures to advance. Still, it is hidden within the presentation of the algorithms.

\ We further provide the following remark to explain what is the main link between the two proposed algorithms.

\ Remark B.1 (LINK BETWEEN K-SIF AND FIF). The first order coefficients of the signature on an interval [s, t] ⊂ [0, 1] represent the displacement of the function:

\

\

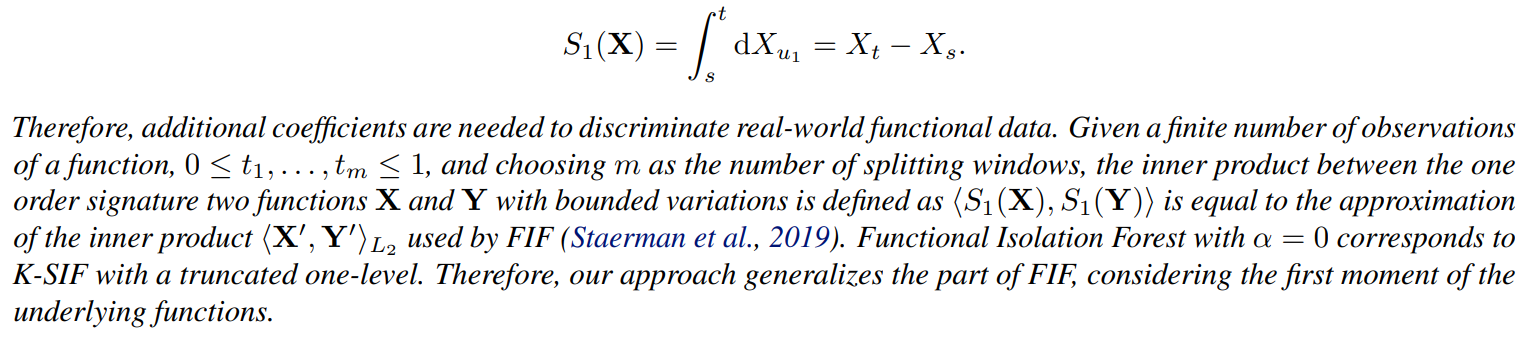
:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\