Revisiting Existing RBN: Developing Riemannian Normalization Approaches Tailored for Manifolds

\

Abstract and 1 Introduction

2 Preliminaries

3. Revisiting Normalization

3.1 Revisiting Euclidean Normalization

3.2 Revisiting Existing RBN

4 Riemannian Normalization on Lie Groups

5 LieBN on the Lie Groups of SPD Manifolds and 5.1 Deformed Lie Groups of SPD Manifolds

5.2 LieBN on SPD Manifolds

6 Experiments

6.1 Experimental Results

7 Conclusions, Acknowledgments, and References

\ APPENDIX CONTENTS

A Notations

B Basic layes in SPDnet and TSMNet

C Statistical Results of Scaling in the LieBN

D LieBN as a Natural Generalization of Euclidean BN

E Domain-specific Momentum LieBN for EEG Classification

F Backpropagation of Matrix Functions

G Additional Details and Experiments of LieBN on SPD manifolds

H Preliminary Experiments on Rotation Matrices

I Proofs of the Lemmas and Theories in the Main Paper

Inspired by the remarkable success of normalization techniques in traditional DNNs, endeavors have been made to develop Riemannian normalization approaches tailored for manifolds. Here we recap some representative methods. However, we note that none of the existing methods effectively handle the first and second moments in a principled manner.

\ Brooks et al. (2019b) introduced RBN over SPD manifolds under AIM, with operations defined as:

\

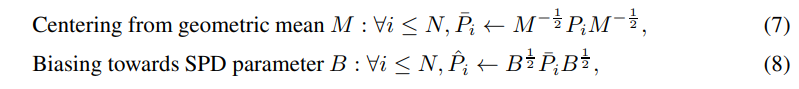
\ where {Pi…N } are SPD matrices, and M are their Frechet mean under AIM. Define a map as

\

\ In summary, prevailing Riemannian normalization approaches lack a principled guarantee for controlling the first and second-order statistics. In contrast, as will be elucidated, our method can govern first and second-order statistics for all Lie groups. We summarize the above RBN methods in Tab. 2.

\

:::info This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.

:::

[2] Although not mentioned in the original paper, Eqs. (7) and (8) can guarantee the mean of the resulting samples under AIM, as Eqs. (7) and (8) are actions of GL(n).

:::info Authors:

(1) Ziheng Chen, University of Trento;

(2) Yue Song, University of Trento and a Corresponding author;

(3) Yunmei Liu, University of Louisville;

(4) Nicu Sebe, University of Trento.

:::

\