Graph structures have been characterized in [3] as the signatures that allow the transformation of the corresponding algebras by the single pushout method. This method is based on the construction of pushouts in categories of partial homomorphisms, defined as standard homomorphisms from subalgebras of their domain algebra, just as partial functions are standard functions from subsets of their domain (in the categorical theoretic sense of the word domain). The results of Section 6 suggest that a similar approach can be followed with monographs. We first need a notion of submonograph, their (inverse) image by morphisms and restrictions of morphisms to submonographs.

\ We may now define the notion of partial morphisms of monographs, with a special notation in order to distinguish them from standard morphisms, and their composition.

\ We now see how these inverse images allow to formulate a sufficient condition ensuring that restrictions of coequalizers are again coequalizers.

\ It is then easy to obtain a similar result on pushouts.

\ We can now show that categories of partial morphisms of monographs have pushouts. The following construction is inspired by [3, Construction 2.6, Theorem 2.7] though the proof uses pushout restriction.

\ Theorem 7.5. The categories of Definition 7.2 have pushouts.

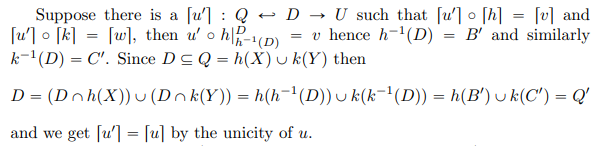
\ If B and C are finite (resp. standard, resp. O-monographs) then so are X and Y, hence so is Q by Theorem 4.4.

\ One important feature of this construction is illustrated below.

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

Feed: Hacker Noon - Medium

View: Original article