LogSumExp Function Properties: Lemmas for Energy Functions

Table of Links

Abstract and 1 Introduction

2 Related Work

3 Model and 3.1 Associative memories

3.2 Transformer blocks

4 A New Energy Function

4.1 The layered structure

5 Cross-Entropy Loss

6 Empirical Results and 6.1 Empirical evaluation of the radius

6.2 Training GPT-2

6.3 Training Vanilla Transformers

7 Conclusion and Acknowledgments

\ Appendix A. Deferred Tables

Appendix B. Some Properties of the Energy Functions

Appendix C. Deferred Proofs from Section 5

Appendix D. Transformer Details: Using GPT-2 as an Example

\ References

Appendix B. Some Properties of the Energy Functions

We introduce some useful properties of the LogSumExp function defined below. This is particularly useful because The softmax function, widely utilized in the Transformer models, is the gradient of the LogSumExp function. As shown in (Grathwohl et al., 2019), the LogSumExp corresponds to the energy function of the a classifier.

\

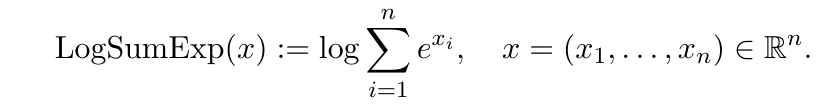
\ Lemma 1 LogSumExp(x) is convex.

\ Proof

\

\

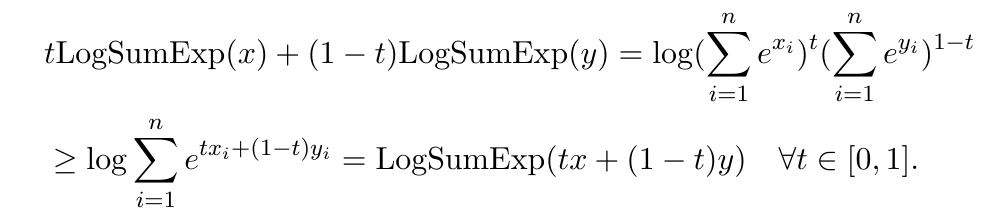
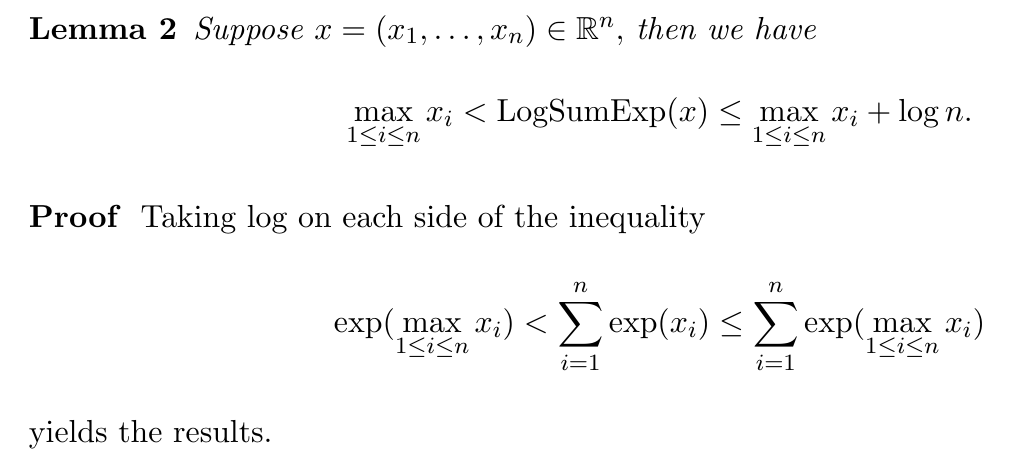
\ Consequently, we have the following smooth approximation for the min function.

\

B.1 Proof of Proposition 2

\

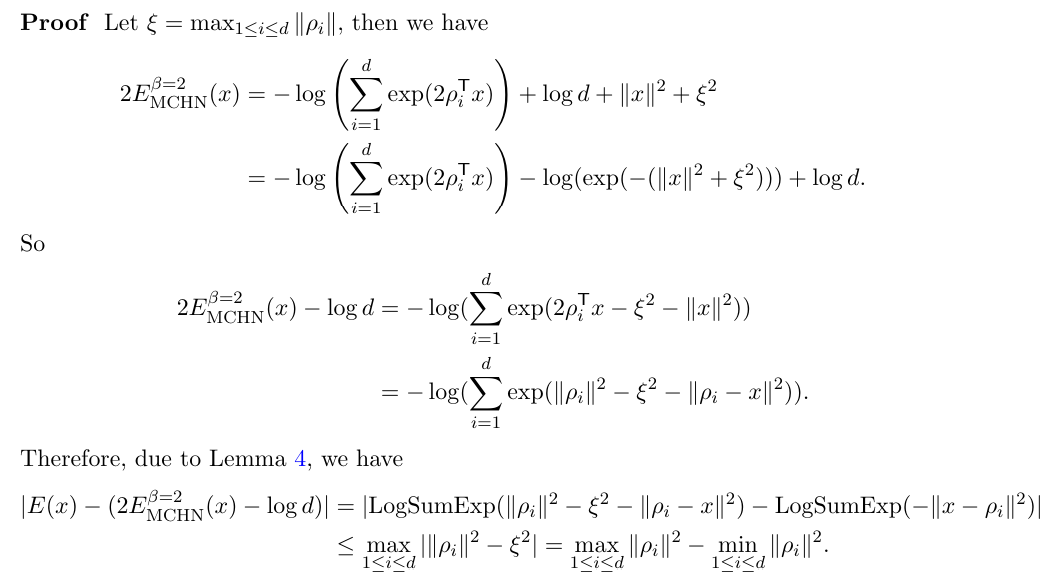
:::info Authors:

(1) Xueyan Niu, Theory Laboratory, Central Research Institute, 2012 Laboratories, Huawei Technologies Co., Ltd.;

(2) Bo Bai baibo ([email protected]);

(3) Lei Deng ([email protected]);

(4) Wei Han ([email protected]).

:::

:::info This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.

:::

\