and the distribution of digital products.
DM Television
Harnessing Shared Security For Secure Cross-Chain Interoperability
With attacks on blockchain bridges leading to billion-dollar losses, it is not surprising that discussions about cross-chain security often generate intense debates. But we believe in taking a more pragmatic approach—one that involves analyzing the problem of secure interoperability from first principles and designing mechanisms to increase safety guarantees for cross-chain applications and their users.
\ In this article, we’ll explore the concept of shared security and explain how shared security designs (like Lagrange State Committees) can reduce the cost of bootstrapping meaningful safety properties for interoperability protocols. While we focus on shared security for cross-chain communication protocols, any decentralized application—irrespective of the use case—can harness this emerging technology to achieve sufficient decentralization and trust-minimization without incurring excessive operational overhead.
An informal introduction to shared security“Shared security” refers to security that a protocol derives from an external source. In a shared security scheme, resources pooled by participants in one protocol (e.g., capital or computational power) are used to create economic security for another protocol. Shared security differs from the standard model where each network is responsible for its security.
\ Public blockchains like Bitcoin and Ethereum, for instance, combine consensus algorithms with Sybil-resistance mechanisms—like Proof of Work or Proof of Stake—to guarantee liveness and simultaneously increase the cost of adversarial attacks (e.g. Sybil attacks, long-range attacks, eclipse attacks, time-bandit attacks, and bribery attacks).
\ Although shared security schemes work differently, the goals usually revolve around two objectives:
- Increasing capital efficiency in blockchain networks without creating additional risk (risk stacking) or introducing additional security assumptions.
- Improving capacity of blockchain networks (especially nascent protocols) to defend against invalid state transitions, re-orgs, censorship resistance, and other against attacks on a protocol’s liveness and safety.
\ Shared security is not exactly a new concept; for example, merge-mining was introduced in 2011, enabling miners to use the same cryptographic Proof-of-Work (PoW) to create blocks on two (or more) different PoW chains implementing Nakamoto consensus. This allowed newer PoW-based protocols (like Namecoin and Rootstock), whose native tokens had not acquired enough value to attract significant interest from miners, to share security by re-using computational resources dedicated to securing the Bitcoin network to increase the difficulty of blocks on the new protocol.
\ That said, merge mining is considered to provide a weak form of economic security for decentralized networks due to its lack of accountable safety. In academic literature, accountable safety reflects a protocol’s ability to detect nodes that (provably) violate protocol rules and punish malicious behavior. For instance, Proof of Stake-based protocols require nodes to lock up collateral (by staking the protocol’s native token) before participating in consensus, and can destroy/freeze (“slash”) this collateral if evidence of a validator’s misbehavior appears.
\ In the case of merge mining, nodes who deliberately accept invalid blocks on the merge-mined chain cannot be reliably detected. Moreover, it is impossible to punish said nodes (even if it were possible to identify them) as that would require a drastic measure like burning or destroying mining hardware. While the threat of the merge-mined chain’s token losing value due to attacks on its security may seem enough to discourage Byzantine behavior, malicious miners have less to lose since the value of the original chain (eg. Bitcoin) is unlikely to be affected.
\ Modern notions of shared security have not only evolved to incorporate accountable safety, but also shifted to using a different unit of investment—capital—as the basis of shared security. In this design, there’s a base protocol that provides security for other PoS protocols built on it; nodes first join the primary network (by locking up the network’s native token as stake) before participating in securing the secondary network.
\ This design can take different forms:
- Validators participate in the primary network and the secondary network simultaneously
- A subset of validators (from the primary network) is randomly sampled to validate and secure the secondary network
- The secondary network is secured by an independent set of validators bonded on the primary network
- Validators from the primary network re-delegate staked capital to validators on the secondary network
\
\ Regardless of implementation details, the crucial detail for the shared security schemes described above is that the base protocol must have the means of punishing validators that act maliciously on the secondary network. Since there is less capital securing the secondary network, the possibility of a malicious supermajority hijacking the protocol is a real concern.
\ The solution is to ensure that one or more honest participants (forming the minority) can hold the majority accountable by initiating a dispute and publishing evidence of protocol-violating behavior to the base layer. If the base protocol (acting as a “judge”) accepts that evidence, the dishonest parties can be punished by slashing collateral (put up as a bond) on the primary network. Importantly, the base layer only has to verify the provided evidence, and does not need to execute additional consensus, before settling disputes—reducing coordination overhead.
\ The more subtle point is that misbehavior must be attributable to some party for slashing mechanisms to be effective. In PoS-based networks, validators are required to generate a public-private key pair that serves as a unique cryptographic identity within the consensus protocol. During routine duties, like proposing blocks or attesting to (the validity of) blocks, a validator signs the block data with its private key—effectively binding it to that choice.
\ This makes it possible to slash a validator for different actions that would be construed as an attack on the protocol’s safety or liveness (or both in some cases):
\
- Signing two conflicting blocks during the same period (formally known as “equivocation”)
- Signing an invalid block (whether during a proposal or attestation)
- Censoring one or more transactions
- Hiding some or all parts of a block’s data
\ While the first two offenses can be detected the same way (by recovering a validator’s public key from its signature), the latter two require other mechanisms like inclusion lists and erasure codes. In all cases, the use of cryptography enables reliable detection and punishment of malicious behavior that could degrade certain desired security properties in a protocol—such as resistance to censorship and validity of transactions. This provides some context on the meaning of “cryptoeconomic security”, which involves combining cryptographic mechanisms with economic incentives to secure decentralized networks.
\ We can illustrate this idea—and compare it to merge-mining—using the example of a new PoS blockchain that shares Ethereum’s security. Our toy protocol has the following properties (note that is an overly simplistic example used for illustrative purposes):
\
- Node operators are required to deposit a specified amount of ETH tokens as collateral in an Ethereum smart contract before enlisting as validators in the PoS network
- During epochs, block proposers on the PoS protocol submit hashes of block headers (which includes signatures of validators) to Ethereum by storing it in a smart contract
- Security is based on fraud proofs—the parent chain (Ethereum) does not verify state transitions, but it can verify a counterexample showing that a particular state transition is invalid
- An on-chain slashing mechanism is activated if a particular state transition is disputed by one or more parties
\ Now, suppose a malicious majority of nodes on the secondary network collude to finalize an invalid block to steal funds deposited in the bridge contract. In this scenario, an honest validator would trigger the on-chain slashing mechanism on Ethereum by publishing a fraud proof and identifying protocol-violating validators. If protocol rules allow for slashing a validator’s entire stake, then the cost of corrupting the PoS chain is proportional to the amount staked by the majority of validators.
\ This example shows how accountable safety underpins shared security designs and effectively allows smaller networks to be secured by bigger protocols that have bootstrapped significant economic security and boast higher levels of decentralization and trustlessness. We can also see that Proof-of-Stake mechanics lead to shared security designs with stronger notions of safety compared to merge-mining (which uses computational power as the basis of economic security).
\ Furthermore, it introduces the idea of a new protocol using another network’s token for staking in order to mitigate the “bootstrapping problem” (where a new blockchain protocol has low economic security because its token has not acquired enough value). While the bootstrapping problem can be solved with approaches—such as merge-mining—that use hardware investment as a unit of economic security, this type of shared security is suboptimal for certain reasons (some of which we have identified previously):
\
- Capital investment—which is supposed to impose significant costs on malicious behavior for validating nodes—is implicit and difficult to leverage for economic security. Making capital investment explicit in the case of PoW merge-mining would require a drastic measure like destroying mining hardware in event of probably malicious behavior, which is unrealistic in real-world situations and difficult to leverage.
- Merge-mining (or any shared security design where participation in consensus is tied to running infrastructure) is difficult to scale. For example, there is an upper bound on how many PoW chains one can merge-mine simultaneously before a miner’s ROI starts to decrease.
\ In contrast, PoS-based shared security schemes that use capital investment as a unit of investment have certain properties that are useful for solving the problem of bootstrapping new networks efficiently and effectively:
\
- Capital investment is explicit (stakers invest capital into buying tokens to meet requirements for collateral) and can be leveraged for strong and concrete guarantees of economic security. For example, it is easy to visualize that a protocol is likely to be more secure when it has 1 ETH worth of stake securing 0.9 ETH worth of transactions than when 0.9 ETH worth of stake is securing 1 ETH worth of transactions.
- Since participation in consensus is tied to “pure” capital investment, it is easier to scale economic security and have validators secure multiple protocols without incurring excessive coordination overhead (especially when hardware requirements are low).
\ Nonetheless, every approach will have drawbacks and shared-security-via-staking is no exception; for example, determining how much collateral validators should put in a PoS protocol is a difficult problem to solve. We’ll put this into context by considering this statement from the preceding paragraph: “It is easy to visualize that a protocol is likely to be more secure when it has 1 ETH worth of stake securing 0.9 ETH worth of transactions than when 0.9 ETH worth of stake is securing 1 ETH worth of transactions.”
\ While this statement sounds reasonable, a deeper analysis reveals the difficulty in choosing an optimal bond requirement:
- Requiring 1 ETH from validators to secure 0.9 ETH worth of assets decreases capital efficiency and results in overcollateralization.
- Securing 2 ETH worth of transactions with 1 ETH worth of stake decreases economic bandwidth (or “leverage”) in a PoS blockchain and results in undercollateralization.
\ In an ideal scenario, a protocol designer would prefer to have 1 ETH of stake securing 1 ETH worth of transactions. But such equilibria are difficult to achieve in real-world conditions for different reasons; for example, the amount of capital to be secured per unit time (a function of the marginal value of transactions per block/epoch) is dynamic. This makes setting the ideal bond in a PoS system a very difficult mechanism problem and an important consideration for stake-based shared security schemes, such as restaking (which we discuss in the next section).
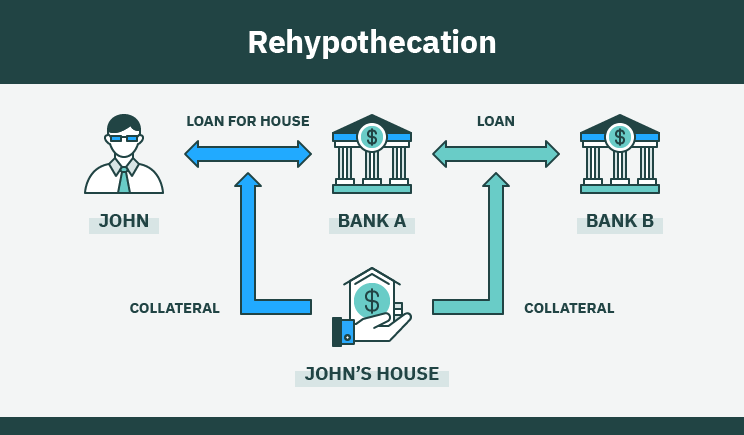
Shared security from restaking and checkpointing RestakingRestaking is rooted in rehypothecation—a practice in traditional finance whereby a lender uses assets (previously pledged as collateral by a borrower) as collateral to secure a new loan. Here, the new counterparty assumes rights to the original collateral asset such that if the entity that took out the new loan defaults on repayment, it can auction off the asset to recoup funds.
\
\ When implemented correctly, rehypothecation can be useful. For starters, it enables higher capital efficiency and liquidity by re-using assets—which would otherwise lay dormant—to secure short-term funding for profit-generating activities. If the profit from taking out a loan exceeds the value of the rehypothecated collateral, all parties involved (the original borrower, the lender, and the lender’s lender) benefit.
\ Rehypothecation involves a great deal of risk (part of reasons the practice has largely fallen out of favor among TradFi institutions), especially for the original borrower who might lose rights to their asset when a liquidation occurs. The lender re-using collateral also bears risk, more so if it’s required to repay borrowers after a new counterparty confiscates deposited collateral due to loan defaults.
\ The other risk is one we’ve briefly described previously and revolves around the overcollateralization vs. undercollateralization tradeoff. In the example highlighted previously, if Bank B (John’s bank) enters an overly leveraged position—where it borrows more than the value of John’s collateral—and suffers a loss, it becomes difficult to pay back the loan from Bank B (or return John’s assets). Bank B may protect against this edge case by asking Bank A (John’s bank) to borrow less than the value of John’s collateral; however, that increases capital inefficiency for Bank A and reduces the gains from rehypothecating John’s collateral in the first place.
\ The same set of pros and cons also apply to restaking. Before going further, it’s important to clarify an important detail: a restaker’s stake always passes through the base protocol first. For example, a restaker on Ethereum will have to either deposit 32 ETH into the Beacon Chain contract or delegate ETH to a validator operated by a staking service—depending on whether native restaking or liquid restaking is used.
\ At a high level, restaking in the case of Ethereum comprises the following:
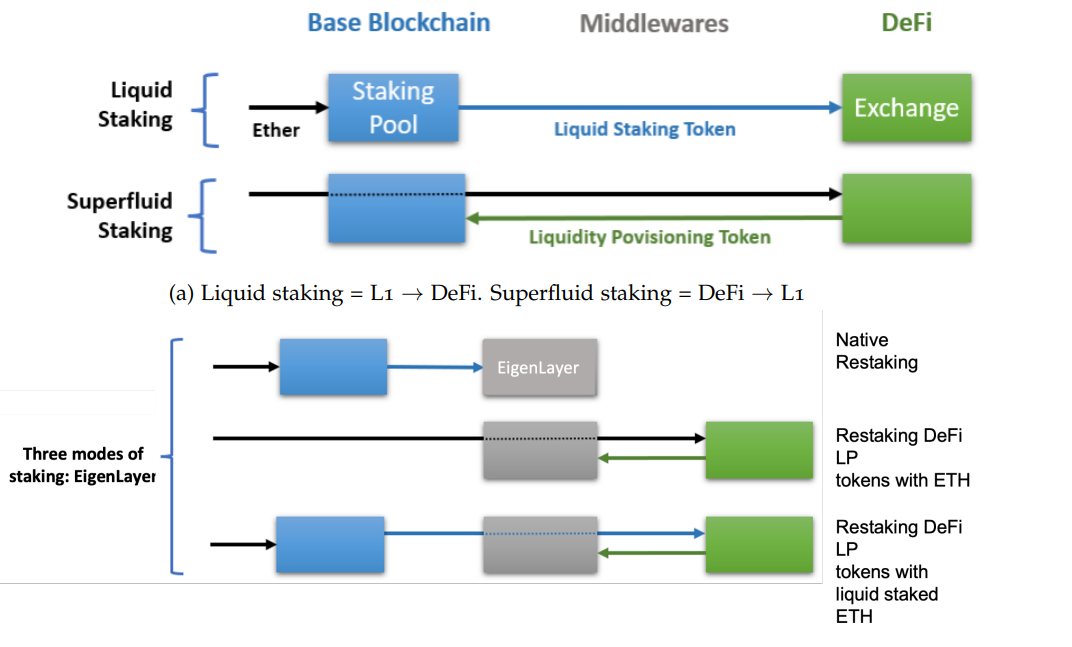
#1: Giving the restaking protocol ownership rights (or a claim) to staked ETHIn native restaking, a validator is required to change their withdrawal address to a smart contract managed by the restaking protocol. Thus instead of funds going directly to the validator after exiting the Beacon Chain, the stake passes through the restaking protocol first before getting to the validator (we’ll see why this is the case soon enough).
\ It is also possible to deposit fungible representations (derivatives) of staked ETH in the restaking protocol’s smart contracts (liquid restaking). Called “liquid staked tokens”, such tokens are issued by staking-as-service operators (eg. RocketPool, Lido, Coinbase, etc.). and represent a claim to a portion of ETH staked by a validator (including yield from rewards) and can be redeemed at 1:1 ratio for native ETH tokens.
\
A restaking protocol usually functions as a “middleware” that various decentralized networks and applications can plug into for economic security. These would typically include protocols that require some form of validation by a set of parties—for example, an oracle network—but whose native token has not accrued enough value to be used in a Proof of Stake setting.
\ Instead of building a new validator set from scratch, such applications can enlist the services of existing validators through a restaking protocol. Services can specify unique slashing conditions on a validator’s rehypothecated collateral—which the restaking protocol can enforce since it now controls the validator’s withdrawal—lowering the barrier to economic security.
\ An important note: AVS slashing conditions are independent from slashing conditions enforced by Ethereum’s Beacon Chain consensus, so a validator’s ETH stake could be slashed even though they did not commit a slashable offense on Ethereum itself. This could lead to what we describe as “risk stacking”: in return for higher capital efficiency, the primary network inherits additional risk than it would otherwise. (Risk stacking also has implications for the core EigenLayer protocol itself as we will see subsequently.)
#3: Receiving additional rewardsRestaking requires taking on significant risk (eg. a restaked validator might be slashed accidentally due to a bug in the on-chain slashing mechanism) But just like rehypothecation unlocks liquidity in TradFi, restaking can improve capital efficiency in PoS ecosystems and generate higher-than-average yield for stakers.
\ This is based on the fact that services who used restaked capital for security are required to reward validators for their services. To illustrate, a restaked validator participating in an oracle network will receive fees for validating oracle updates—with payment coming from other third-party applications that rely on the oracle’s services. With validators still receiving rewards from the Beacon Chain, restaking enables earning income from multiple PoS protocols without having to re-deploy fresh capital to a new ecosystem.
\ Though we focus on Ethereum restaking in this example, other Proof of Stake protocols have also implemented variants of restaking to achieve similar objectives (reducing the cost of launching new protocols/applications, improving capital efficiency, and scaling economic security). In fact, the next section discusses EigenLayer—Ethereum’s premier restaking protocol—before proceeding to highlight restaking in other ecosystems:
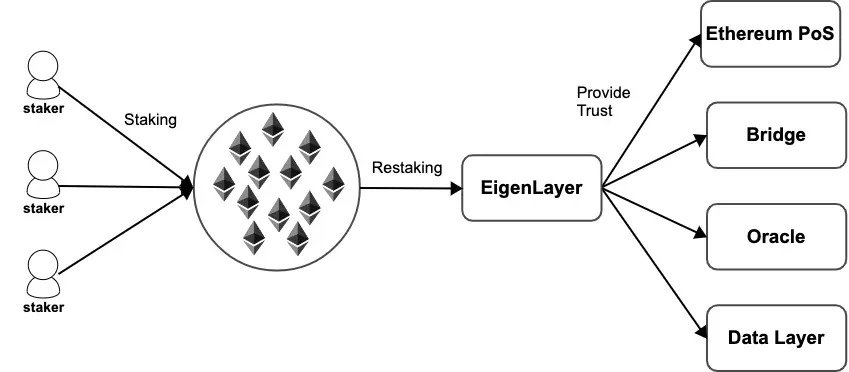
EigenLayerEigenLayer is a restaking protocol created to extend Ethereum’s economic security to secure new distributed applications, networks, and protocols (which it collectively describes as “Actively Validated Services” or AVSs for short). If you’ve read the previous section describing the example of restaking on Ethereum, then you already understand EigenLayer’s operations at a high-level; however, we’ll include some more details for context.
\
\ After restaking ETH (by pointing withdrawal credentials associated with a validator to smart contracts controlled by EigenLayer), a validator is required to perform tasks specified by the AVS they wish to operate. For instance, if an AVS is a sidechain, the restaked validator must run client software for the sidechain to execute transactions and verify blocks, while earning rewards for carrying out these tasks correctly. More broadly, tasks can vary depending on the nature of the AVS:
\
Storing data in a data availability network
Approving deposit and withdrawal transactions for a cross-chain bridge or approving messages for a cross-chain messaging protocol
Generating and verifying zero-knowledge proofs for a privacy-focused application or shielded payments network
Storing and verifying block headers and running relayers/oracles for cross-chain interoperability protocols
\
Astute readers will notice two things: (a) tasks specified by an AVS can be quite arbitrary (b) different AVS-specified tasks require varying levels of investment and effort. To illustrate the latter point, it is possible to imagine that storing block headers in a cross-chain protocol will require less disk/memory space compared to storing and provisioning data in a data availability network (even where techniques like data availability sampling reduce storage burdens on individual nodes).
\ This is one reason EigenLayer allows for restaked validators to delegate execution of AVS-specified tasks to another party (an operator) who shares rewards earned from the AVS with the validator. This approach has varying levels of risk for restaked validators depending on the extent to which the burden of slashing—which can happen if the operator fails to carry out AVS tasks correctly—is shared between the restaked validator and the third-party operator.
\ Each AVS specifies a set of conditions under which an EigenLayer restaker’s stake can be slashed. For instance, a data availability network implementing Proof of Space/Storage mechanisms may slash operators that fail to store data for the agreed duration. Slashing triggers freezing of the operator within EigenLayer—preventing further participation in one or more actively validated services—and eventual reduction of the validator’s ETH balance.
\ For slashing to occur, the offense must be provable—which is what allows the base protocol (Ethereum in this case)—to adjudicate disputes and punish the dishonest party. Ethereum’s current design permits slashing up to 50% of a validator’s stake (16 ETH), which leaves EigenLayer with rights to slash the remaining 50% (16 ETH) in event of an operator breaking rules specified by the AVS while executing tasks.
\ EigenLayer’s slashing mechanics also hints at a subtle risk of restaking: getting slashed by one service reduces a validator’s overall balance in EigenLayer smart contracts and Ethereum’s Beacon Chain. Importantly, an edge-case scenario appears, however, when slashing occurs due to a bug in the slashing logic of a particular AVS and not as a result of a provable offense. In this case, the loss of rewards from validating the main Ethereum chain—assumed to be higher than rewards from validating the AVS—would make the ROI from restaking suboptimal from a validator’s perspective.
\ Another risk with EigenLayer-style restaking concerns the risk of validator overcollateralization and undercollaterilaztion and the concept of risk stacking. From the previous example of rehypothecation, we see that the party rehypothecating collateral may be simultaneously indebted to the first borrower (whose collateral is used to take out a new loan) and the final lender in the chain (who has a claim on the collateral pledged by the original borrower).
\ A similar dynamic can play out in restaking constructions like EigenLayer if a restaked validator (willfully or deliberately) simultaneously commits slashable offenses on Ethereum’s Beacon Chain and one or more AVSs. Depending on where the first slashing occurs, other AVSs may have no stake left to slash—effectively enabling a risk-free attack on applications secured by EigenLayer.
\ The EigenLayer team has acknowledged this attack vector (see Appendix B: Cryptoeconomic Risk Analysis of the EigenLayer whitepaper) and has made several steps to address this risk. This includes providing a formal heuristic for assessing staker undercollateralization and overcollateralization in AVSs, and indicating plans to supply advisory information to AVS developers via a risk management dashboard at launch.
Polkadot Parachains\
\ Although mostly known for enabling interoperability between heterogeneous blockchains, Polkadot relies heavily on shared security. In fact, shared security is the reason different chains in Polkadot’s ecosystem can exchange messages without introducing trust assumptions or incurring security risk.
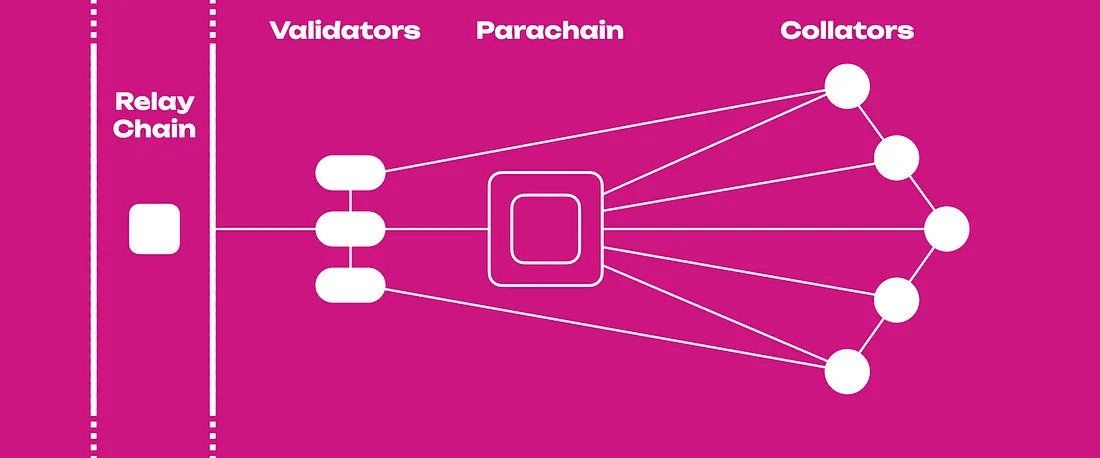
\ On Polkadot, subsets of validators (having staked DOT tokens on the Relay Chain) are randomly assigned to parachains (think “child chains”) to verify blocks—and the associated Proof of Validity (PoV)—produced by each parachain’s collator. A collator is the node responsible for executing a parachain’s transactions and creates a “para-block” sent to the parachain’s validator group for verification.
\ As verifying a block’s PoV is computationally intensive, para-validators (the name for validators assigned to a parachain) receive additional rewards for this duty. Blocks approved by para-validators—or more accurately, cryptographic commitments to those blocks—are sent for inclusion into the Relay Chain (think “parent chain”). A parachain block becomes final if a block referencing it is approved by a majority of the remaining set of validators on the Relay Chain.
\ The last point is quite important: as the number of validators on each parachain is low (around five validators per shard), the cost of corrupting individual shards is low. To defend against such attacks, the Polkadot protocol requires para-blocks to undergo a secondary check by another group of randomly selected nodes.
\ If a block is proven to be invalid or unavailable (ie. some part of the data is missing), honest nodes can initiate a dispute on the main Relay Chain in which all Relay Chain validators are required to re-execute the disputed block. A dispute ends after a ⅔ supermajority of validators vote for either side of the dispute, with the offending validators getting slashed on-chain if re-execution supports the slashing claim.
\ This mechanism ensures that all parachains in the Polkadot protocol share the same level of security, irrespective of the size of the validator set on each shard. Moreover, parachains derive security from the same source (all para-blocks are approved by the Relay Chain), they can trust the validity of messages originating from a remote shard (without necessarily knowing details of the latter’s consensus or state).
Interchain Security\
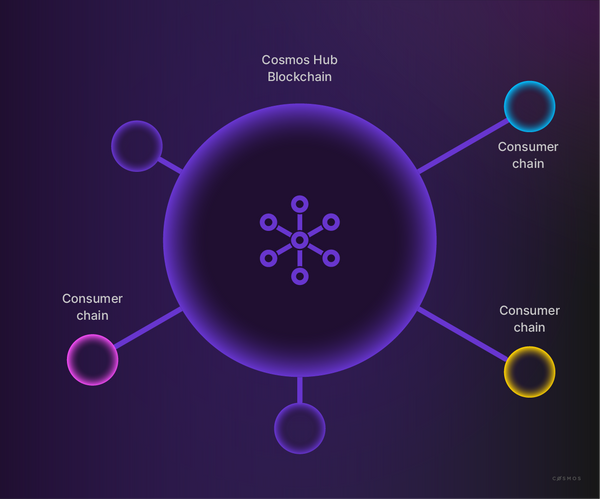
\ Interchain security has been described as Cosmos’s answer to restaking and bears similarity with Polkadot’s shared security model. Similar to the relationship between the Relay Chain and parachains on Polkadot, Cosmos adopts a hub-and-spoke model where multiple chains (“Cosmos Zones”) connect to a main chain (the “Cosmos Hub”) and derive security from it. The rationale is also similar to Polkadot’s: enable new chains to remain secure without needing to bootstrap a reliable validator set from scratch (a fairly difficult task) and instead share economic security—pooled on a single layer—with other chains.
\ In its current iteration, interchain security requires a validator (having staked ATOM tokens) to validate both the Cosmos Hub and all consumer chains connected to it. A validator acting maliciously on a consumer chain risks losing their stake on the provider chain (the Cosmos Hub in this case) to slashing.
\ Slashing an offending validator typically requires relaying a packet containing evidence of slashable behavior via the IBC (Inter-Blockchain Communication) channel between the provider chain and the consumer chain. Thus, interchain security can be seen as a form of restaking; plus, it achieves a critical objective: making it easier to launch application-specific blockchains in the Cosmos ecosystem.
\ Previously, projects attempting to create sovereign blockchains were required to create a native token for staking and attract a sufficient number of validators to provide new users with minimum guarantees of safety. However, interchain security ensures the security of the Cosmos Hub (secured by ~$2.5b in stake at the time of writing) can be scaled to secure newer, low-value chains without needing to expand the size of Cosmo’s existing validator set.
\ Note: The current version of Cosmos’s Interchain Security disables slashing based solely on packets relayed by consumer chains due to the risk of malicious code on a consumer chain triggering transmission of fake slash packets and slashing honest validators—instead offenses like double-voting (signing two blocks at the same height) are subject to social slashing via governance. Social slashing comes with its own risks, however, as seen in the recent debate over slashing validators for double-signing on a consumer chain (which also hints at some of the complexities of building out shared security protocols).
\ Mesh security is an alternative to interchain security and seeks to improve some of the latter’s shortcomings. Instead of running software for both provider and consumer chains, a validator staked on the provider chain can delegate stake to a validator on the consumer chain. This lifts the burden of validating two chains simultaneously—participating in governance and consensus—and reduces overhead for restaked validators (eg. reducing hardware requirements).
\ Just like EigenLayer (where an Ethereum validator can have an operator validate one or more secondary protocols (AVSs) on its behalf), a delegate validator is not required to put up any stake validating the consumer chain. If the delegate validator fails to carry out duties correctly (e.g., suffering downtime or creating/voting for invalid blocks), the delegator is slashed on the consumer chain per the protocol’s rules.
\ Mesh security is also different from interchain security as it allows consumer chains to lease security from multiple provider chains (instead of being restricted to the Cosmos Hub) and permits validators to choose what chains to delegate stake to. While the latter feature is planned as part of the ICS v2 rollout, the former is unlikely to be implemented (though is arguably more compelling).
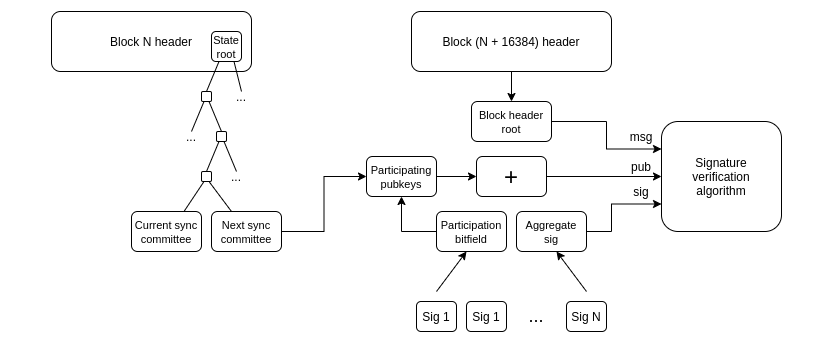
Ethereum’s Sync CommitteeEthereum’s Sync Committee is a group of 512 validators responsible for signing off on finalized Beacon block headers. A new Sync Committee is reconstituted every 256 epochs (roughly 27 hours), with members selected from the Beacon Chain’s existing validator set. Note that members are expected to continue regular validator duties (including attestation and block proposals) whilst participating in the Sync Committee.
\ The Sync Committee was first implemented during the Altair fork of the Beacon Chain to enable light clients to verify new blocks (without knowing the full validator set) and track changes in Ethereum’s state. Since participating in the Sync Committee requires more effort than simply partaking in Beacon Chain consensus, members receive a small reward (in addition to regular rewards for completing Beacon chain duties).
\
\ However, members who sign off on invalid block headers are not subject to slashing—unlike on the Beacon Chain. Ethereum’s core devs have defended this design by saying slashing malicious Sync Committee members would introduce more complexity, while others have hinted at the difficulty of collusion among the ⅔ supermajority of Sync Committee members (what it’d take to trick light clients into accepting a bad block header).
\ But with high-value applications—such as cross-chain communication protocols—relying on light clients to track Ethereum’s state, the topic of slashing Sync Committees for signing invalid block headers has attracted renewed interest (cf. an ongoing proposal by the Nimbus client team). If implemented, slashing would turn participation in the Sync Committee into a form of restaking whereby validators opt in to additional slashing conditions and receive extra rewards for the secondary service of signing block headers.
\ To illustrate, a validator could be slashed—up to their maximum balance—if they violate protocol rules while in the Sync Committee, even if they act honestly while participating in the Beacon Chain’s consensus. We can also compare the Sync Committee to to Polkadot’s parachain system and other forms of shared security that randomly sample a subset of nodes to validate a subprotocol within the larger blockchain network (e.g., Lagrange State Committees, Avalanche’s Subnets, and Algorand’s State Proofs protocol).
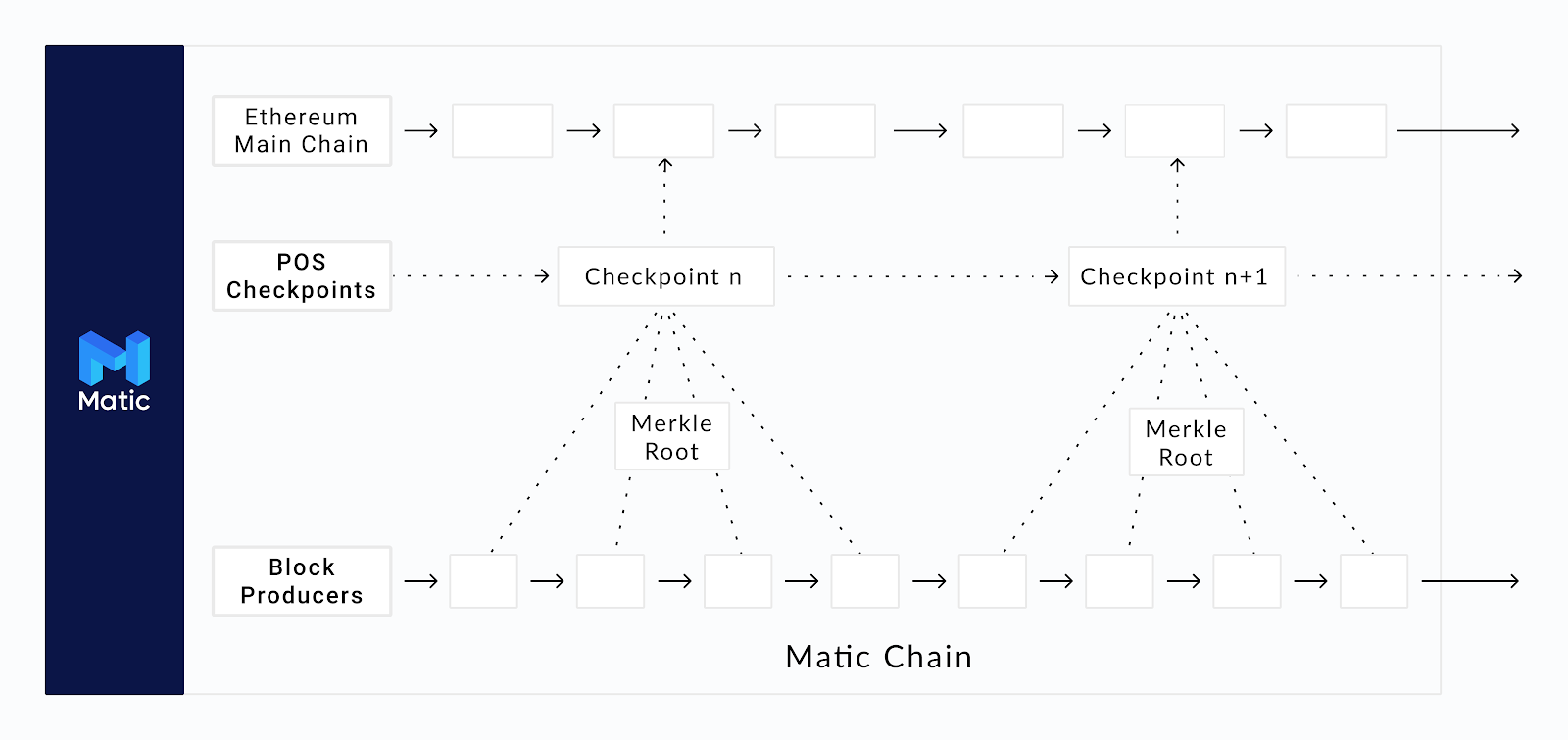
CheckpointingShared security schemes based on checkpointing often involve a security-consuming chain posting cryptographic commitments to its latest state to the security-providing chain at intervals. For example, a block proposer may be required to post the hash of the newest block header to the parent chain before it is finalized.
\ These commitments are described as “checkpoints” because the parent chain guarantees the irreversibility of the child chain’s history leading up to that point. In other words, the parent chain guarantees and enforces a (canonical) time-ordering of the child chain, protecting it against attempts to re-organize blocks and create a conflicting fork (eg. to revert old transactions and perform a double-spend).
\ The parent chain may also guarantee validity of the child chain, especially where block headers have information about who attested/produced a particular block. If a block turns out to be invalid, an honest node can start a challenge on the parent chain (with the parent chain arbitrating the dispute) and trigger a rollback of the child chain’s state.
\ Also, if a mechanism for managing validator stakes (like a smart contract) is implemented on the parent chain, it becomes possible to enforce accountable safety by slashing protocol-violating validators after a valid proof of fraud is accepted on-chain. That the parent chain guarantees the child chain’s canonical history is important here since it prevents nodes from rewriting history (by removing blocks) to hide evidence of malicious behavior.
\ Commit sidechains (Polygon PoS), optimiums (Arbitrum Nova/Metis), rollups, and chains integrated with checkpointing protocols like Babylon implement this form of shared security. In all cases, a protocol derives its economic security from an external blockchain chain by using it as a settlement layer (responsible for finalizing blocks). For context, Polygon PoS and Arbitrum Nova/Metis store headers in an on-chain contract on Ethereum, while Babylon streams headers from connected Cosmos Zones to Bitcoin.
\ Layer 2 (L2) rollups utilize a similar mechanism (posting block roots to the Layer 1 blockchain), with a crucial difference: the data required to recreate a rollup’s blocks is also published on the settlement layer. This means the settlement layer fully guarantees the rollup’s security (eventually). In contrast, the data required to reconstruct the state of a commit sidechain or optimistic chain may be unavailable—particularly in the case of a malicious sequencer or validator set performing data withholding attacks.
Shared security for cross-chain interoperability protocolsHaving provided extensive background on the meaning and evolution of shared security, we can now delve into new frontiers in shared security designs. One such area of research is shared security for cross-chain protocols, which seeks to enhance current approaches to messaging and bridging between blockchains by harnessing the benefits of pooled (economic) security.
\ This definition may bring up questions in the reader’s mind, such as:
Why the explicit focus on interoperability protocols?
What benefits does an interoperability protocol derive from integrating with shared security technology?
\
Lagrange Labs is building Lagrange State Committees—a shared security solution for protocols that require access to trust-minimized proofs of cross-chain states. (State Committees combine Lagrange’s ZK Big Data proof system and EigenLayer’s restaking infrastructure to create a shared zone of security for cross-chain interoperability protocols.) As such, we feel compelled to dissect each of the previous questions, and in the process, make the case for integrating bridging, indexing, and messaging applications with State Committee infrastructure.
A brief primer on interoperability protocolsIn Interoperability For Modular Blockchains: The Lagrange Thesis, we explained that interoperability protocols are crucial for connecting siloed blockchains and mitigating problems around fragmentation of liquidity and state for blockchain applications (and their users). Some key examples mentioned in that article include:
\
Bridges that implement lock-and-mint or burn-and-mint mechanisms and permit transferring an asset from a native blockchain (where it was issued) for use on a non-native blockchain
Messaging protocols that allow users to securely relay information (via data packets) between blockchains that do not share a single source of truth and are unable to verify each other’s states
\
We also highlighted the value of different types of blockchain interoperability solutions. For example, bridges enable users to move seamlessly between different ecosystems, gain exposure to more applications, and increase efficiency of assets (by taking advantage of yield-generating opportunities that exist on other blockchains). Messaging protocols also unlock more advanced use cases like cross-chain lending, cross-chain arbitrage, and cross-chain and cross-chain margining that rely on transferring information (e.g., positions and debt profiles) between various domains.
\ Though designed for different purposes, all different interoperability solutions all share some basic properties. The most important is a mechanism for verifying that some information about the blockchain(s) involved in a cross-chain transaction/operation—provided by the user or an application—is true. This is typically a claim that a particular state (eg. values stored in a smart contract's storage, the balance of an account, or the most recently finalized block) exists, or that a transaction occurred on a different chain.
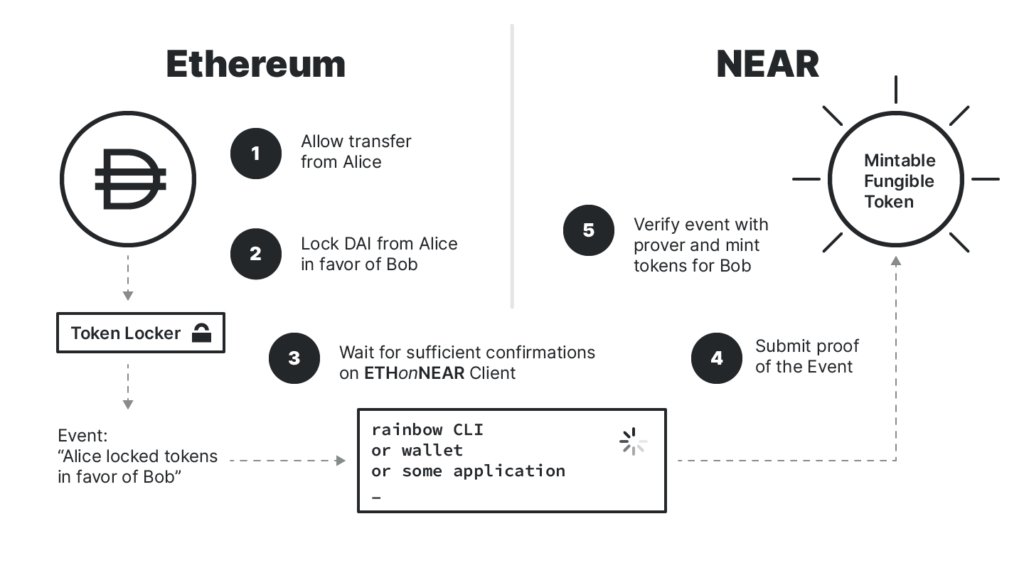
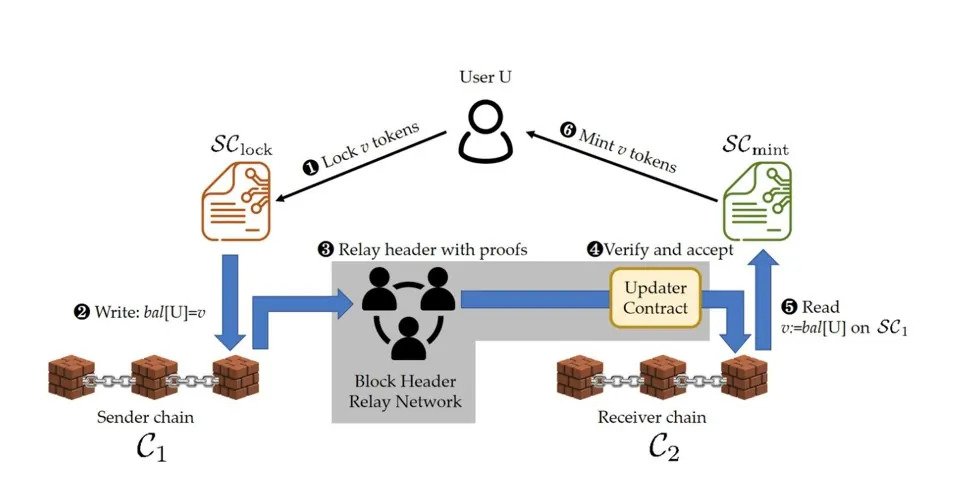
\ Take the example of a bridge between Ethereum and NEAR; the bridge’s operator will need to validate the following information about the state of each chain when a user is bridging an asset (e.g., DAI):
- Before minting nearDAI tokens to the user’s NEAR address, the bridge operator needs proof that said user deposited DAI to the bridge’s contract on Ethereum
- Before releasing the original DAI deposit (when bridging from NEAR to Ethereum), the bridge operator needs proof that said user burned nearDAI tokens on NEAR and sent the required “proof-of-burn” receipt to the bridge’s contract on NEAR
\
\ A messaging protocol between the aforementioned chains will have similar, but slightly different, requirements. If an Ethereum user requests the execution of a cross-chain transaction (“call X contract on NEAR”), the protocol must verify that the message request was originally placed on Ethereum (typically by calling an on-chain contract).
\ A straightforward way to validate claims about cross-chain transactions is to run a full node for the chain in question. Full nodes that download transactions from each block and re-execute before syncing the chain's latest state are typically the most trustless way of verifying state transitions on any blockchain. However, running a full node is both arduous and unnecessary; arduous because full nodes require high hardware requirements, and unnecessary because a cross-chain protocol just needs information relevant to some sets of transactions and contracts.
\ Fortunately, light clients provide an easy/effective way to track events and state changes without requiring the running of a full node. Provided we trust the design of the light client, we can simply download block headers to verify specific information like the occurrence of deposits/withdrawals in a bridge and status of message requests/execution in a messaging protocol.
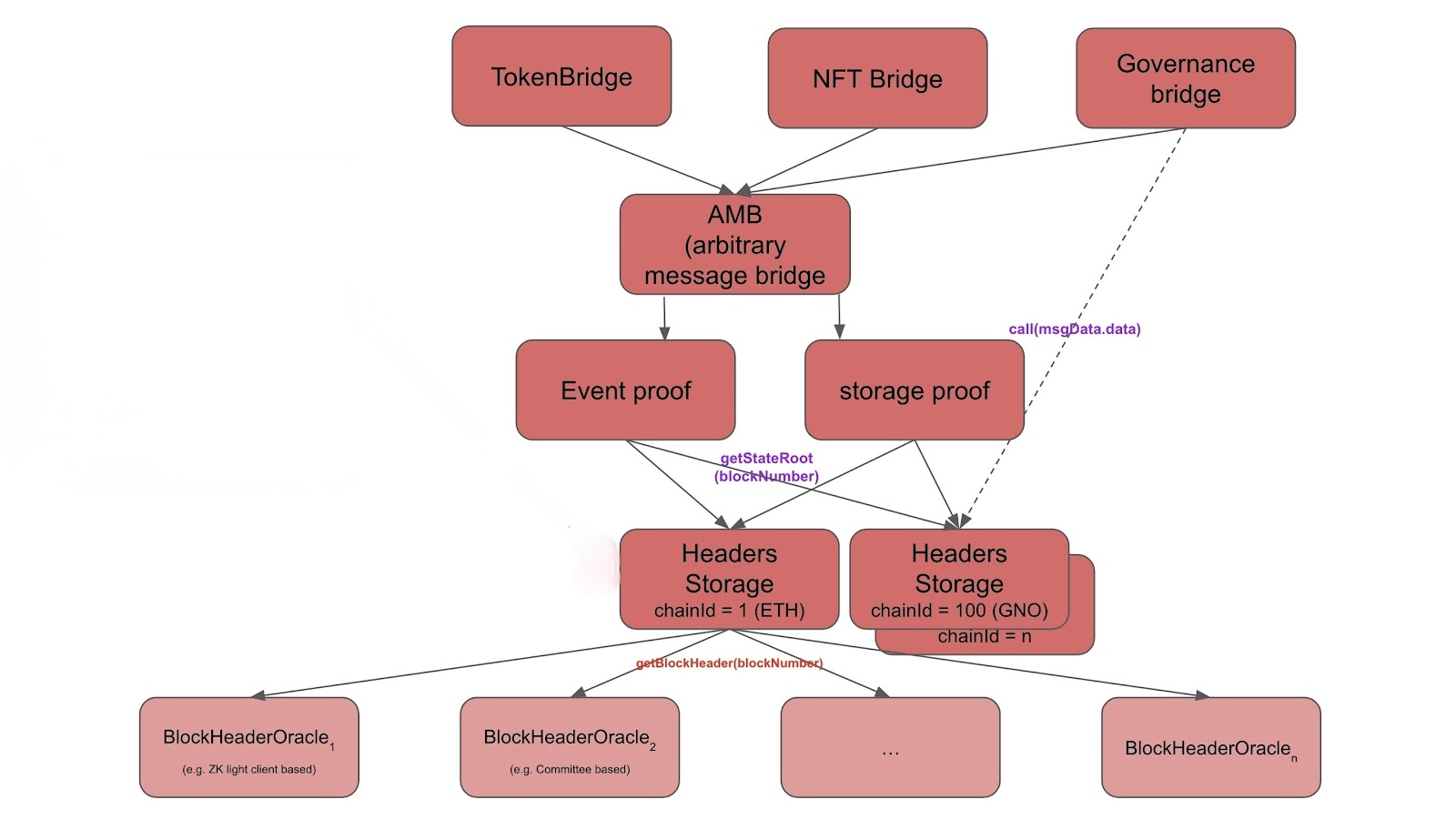
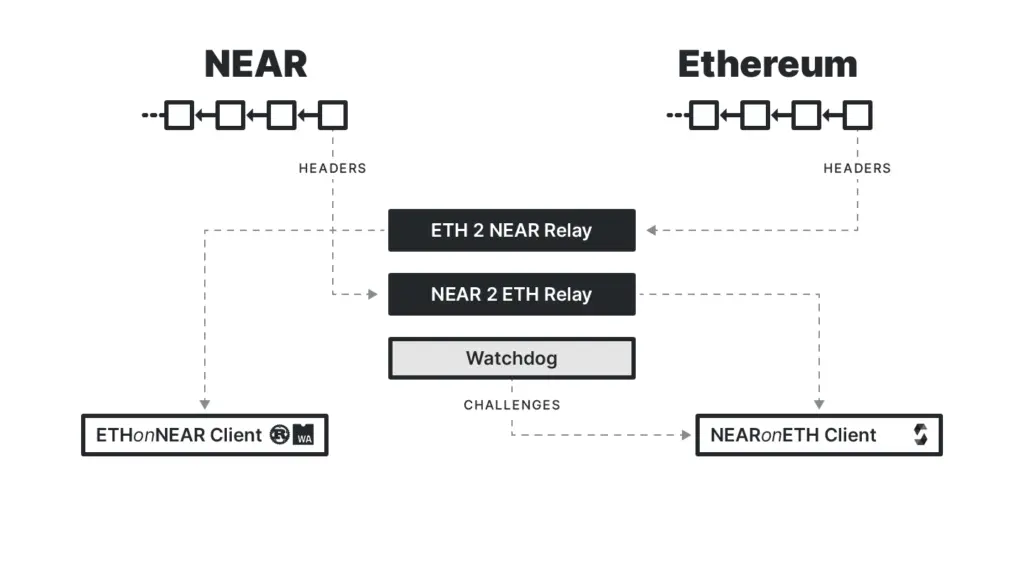
\ To enable communication between two chains—which we’ll call chain A and chain B—an interoperability protocol would run a light client of chain A on chain B that stores block headers of chain B (and vice versa). This enables it to verify various proofs of state/storage (block headers, Merkle proofs, etc.) passed by users (or any third-party) from an application on the source chain to another application on the destination chain. The light client functions as a source of information (an “oracle”) about the states of the two blockchains as illustrated in the image below:
\
\ However, this approach to verifying validity of cross-chain states runs into the problem of trust. Vitalik Buterin’s article Trust Models provides a concise definition of trust: “Trust is the use of any assumptions about the behavior of other people.” The article also defines the concept of trustlessness (with a caveat):
\
One of the most valuable properties of many blockchain applications is trustlessness: the ability of the application to continue operating in an expected way without needing to rely on a specific actor to behave in a specific way even when their interests might change and push them to act in some different unexpected way in the future. Blockchain applications are never fully trustless, but some applications are much closer to being trustless than others. — Vitalik Buterin
\ In our context (blockchain interoperability), trust becomes inevitable when the state of two or more chains are validated independently of each other. Consider a scenario where Bob’s application on chain A receives a proof that Alice initiated a message (“lock 5 ETH on chain B and mint 5 Wrapped ETH (WETH) on chain A”). The message proof is a Merkle proof showing the inclusion of Alice’s transaction in a block, which Bob—because he runs an on-chain light client for chain B—can verify by comparing the proof against the Merkle root of transactions derived from the header of a valid chain B block.
\ However, “valid” in the context of a block can mean different things: (a) “The block header belongs to a block approved by a majority of the source chain’s validators.” (b) “The block header belongs to a block whose transactions are valid according to the source chain’s transaction validity rules.”
\ Bob can to treat #1 as a concrete proof of a block’s validity, but this is based on assumptions about the validators on the source chain:
- “The majority of validators on chain A are honest and would not approve a block with one or more invalid transactions.”
- “The majority of validators on chain A are economically rational actors and have low incentives to approve a block with invalid transactions.”
\ Here, it’s easy to see where either (or both) of these assumptions can break down—for instance, if the amount of stake < value of transactions on chain A (e.g., the amount that can be stolen from a bridge via fraudulent transactions), validators have incentive to finalize an invalid block—even if it means getting slashed—since the profit from an attack outweighs the costs.
\ In general, every mechanism for verifying cross-chain states is subject to trust assumptions (we’ll discuss some of these trust assumptions in detail). The key objective—and this is a theme that recurs throughout this article—is that we want to minimize trust in cross-chain communication to a level where various trust assumptions do not represent a great security risk for interoperability-focused applications.
\ This is an important objective because, as it turns out, when you build an interoperability protocol to link different blockchains, and an application running on one side of the divide accepts a false claim that some arbitrary event happened on the other side, bad things—really bad things—can happen. To illustrate, bridge exploits have happened because a bug enabled savvy hackers to successfully forward (fake) proofs of non-existent message requests and mint tokens on a destination chain without depositing collateral on the source chain.
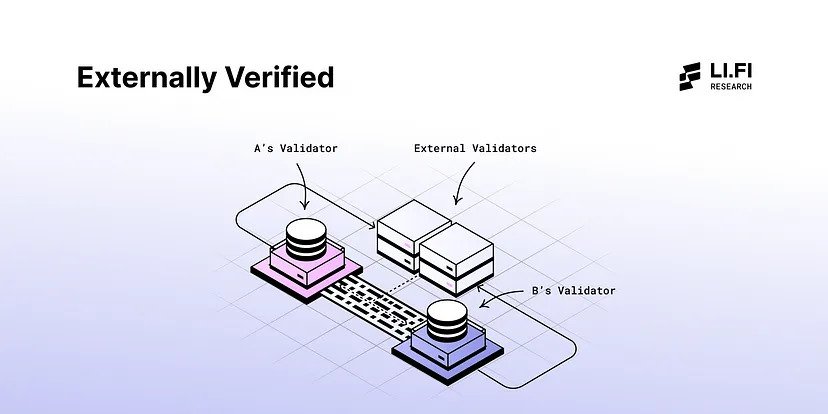
Analyzing existing cross-chain security mechanismsProtocol designers have since come up with solutions to the problem of validating information in cross-chain communication; the most common being the use of a third party to verify the existence/validity of a cross-chain transaction. The rationale is simple: an application on chain A might be unable to verify the state of chain B, but we can have it verify that a group of people (whom we trust or expect to be honest through some mechanism) have validated a piece of information (or claim) referencing the state of chain B.
\ This is called “external verification” since another party external to the blockchain acts as a source of truth for on-chain events and (typically) involves one or more verifiers executing signatures on block headers from the source chain. Once the application on the destination chain receives this signed header, it can then verify various state proofs provided by a user (balances, events, deposits/withdrawals, etc.) against it.
\
\ To establish some level of fault tolerance, some interoperability protocols use a threshold signing scheme that requires a minimum number of private keys to execute a signature for validity (multisignature and multiparty (MPC) wallets are common examples). But having a plurality (k of n) or of verifiers attest to cross-chain states isn’t exactly a silver bullet for security, especially for small sets of verifiers.
\ For example, someone might compromise just enough signers in a multisig scheme and proceed to authorize fraudulent withdrawals out of a cross-chain bridge. An MPC setup is slightly more secure (the approval threshold can be changed and keyshares rotated more frequently), but is still susceptible to attacks (especially in cases where one party controls the majority of keyshares).
StakingOne way to reduce trust assumptions for interoperability protocols and enhance safety of cross-chain communication is to have external verifiers stake collateral as a bond before assuming verification duties. Staking creates security for externally verified systems, particularly as bonded collateral can be slashed if a verifier node executes a signature on an invalid block header or approves an invalid cross-chain transaction).
\ But even this approach comes with problems depending on whether staking is permissioned or permissionless. A permissioned system (where validators must be whitelisted) is often restricted to a few pre-approved entities and is easier to develop—no need to invest in extensive incentive design, especially where validators are publicly known and have incentive to act honestly to preserve their reputation. It is also efficient since communication—necessary for reaching consensus—occurs between few parties who already know themselves.
\ Of course, having a permissioned system with identifiable participants opens up the door for adversarial attacks; for example, an attacker might successfully impersonate or bribe some of these validators and thereby assume majority control. Worse, a Proof of Authority (PoA) system wherein validators are not actually staked (and are simply appointed) reduces the cost of attacking the system to zero (attackers can simply compromise PoA validators through social engineering schemes and hijack the system, for example).
\
\ A permissionless staking system increases the cost of corrupting a system by allowing any interested party (with the right amount of capital) to start validating cross-chain operations. If combined with a consensus protocol that requires ≥ ⅔ majority to attest to block headers, the cost of corrupting the system would effectively equal the minimum amount required to corrupt the majority of verifiers in the system. Plus, users have fewer trust assumptions (validators can be slashed), and a dynamic set of verifiers increases the difficulty of compromising specific nodes through techniques like social engineering.
\ What could possibly go wrong? A lot, actually. For starters, the amount of stake securing the system must be equal to or higher than the total value of assets at risk if a security incident (degrading the interoperability protocol’s safety or liveness) occurs. If the reverse is true (total stake securing the system < total value at risk), then even the threat of slashing becomes ineffective at guaranteeing security since the profit from corrupting the system outweighs the cost of corrupting it.
\ Furthermore, trying to implement the aforementioned security property would likely require setting higher stake requirements for prospective validators. This in turn introduces the problem of capital inefficiency—since security relies on validator nodes doing two things:
\
Depositing a lot of money upfront (as stake) before participating in validation duties
Leaving the money unused for a long period (for safety, PoS protocols impose lengthy delays on withdrawals—some as long as weeks or months—to prevent edge cases where a validator commits a slashable offense and attempts to withdraw immediately to avoid losing funds to slashing)
\
Another thing we have not mentioned is the burden on developers who must now reason about cryptoeconomic incentives to discourage dishonest behavior and design complex staking functionality for the protocol’s token. Besides taking away attention from more important activities—like product development and community engagement—it also adds to the complexity and cognitive overhead of the development cycle for teams building out interoperability infrastructure.
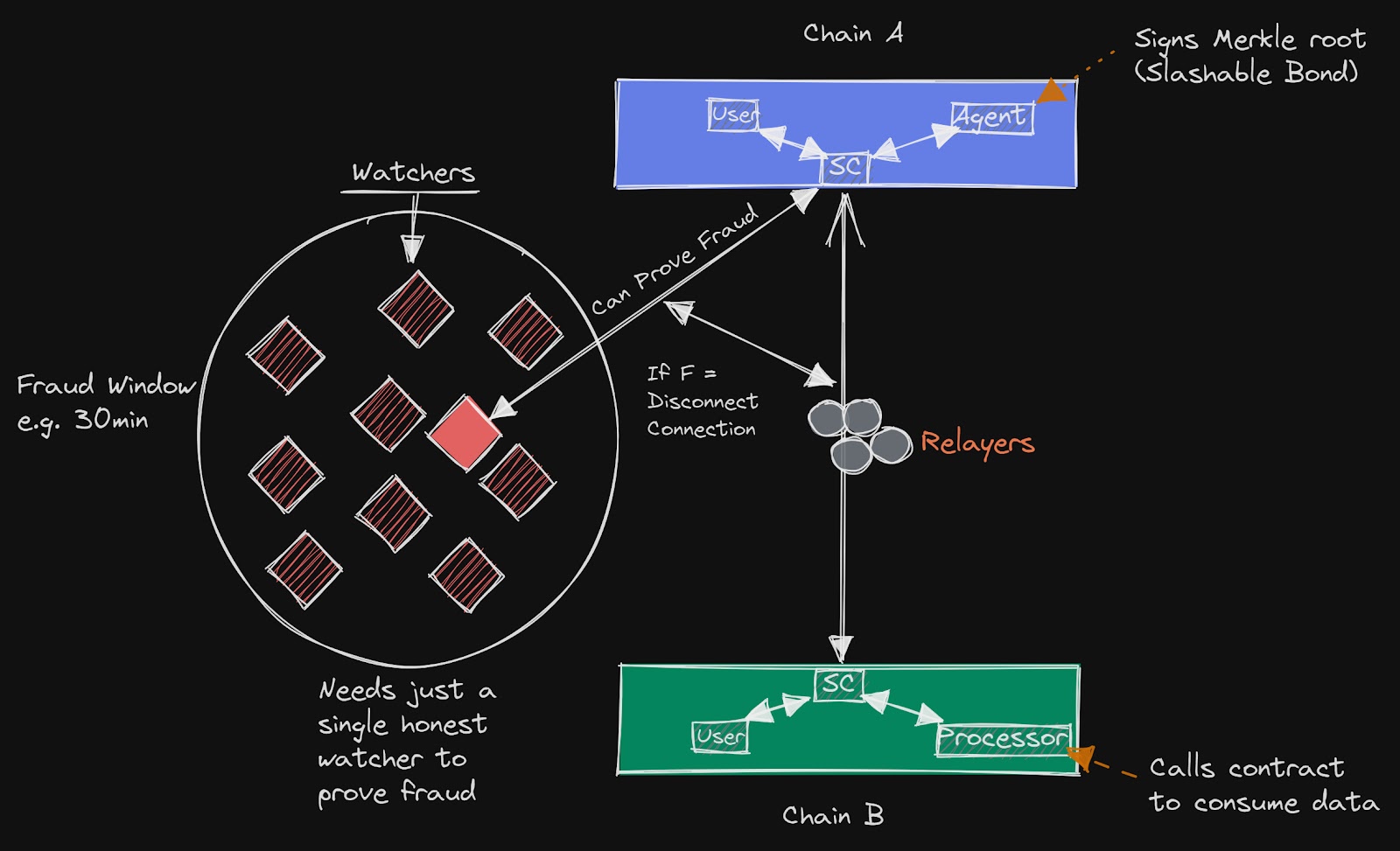
Optimistic verification“Optimistic verification” is another take on the problem of cross-chain security: instead of asking a trusted party or group to attest to cross-chain state, we allow anyone to do it. Crucially, the party making claims about cross-chain states to a client interoperability application (usually called a “relayer”) is not required to provide proof that the attested state is valid. This comes from the “optimistic” assumption that relayers will act honestly and only make valid claims about cross-chain states.
\ But of course, we fully expect one or two (or more) relayers to go rogue, which is why optimistically verified systems require relayers to post a small bond before submitting state proofs. The execution of transactions—those that reference cross-chain states reported by a relayer—is also delayed to give anyone watching the system enough time to dispute invalid claims within the challenge period. If a relayer’s claim turns out to be invalid, the posted bond is slashed—with some part of it going towards the challenger.
\
\ Optimistic verification turns the problem of having to trust a plurality (k of n) or majority (m of n) verifiers into the problem of trusting one verifier (1 of n) to act honestly. For optimistically verified protocols to remain secure, it suffices to have one actor who has enough state data to re-execute transactions and create fraud proofs to challenge fraudulent transactions within the delay period (hence the 1 of n security assumption).
\ This reduces overhead since the system can operate correctly with a single relayer (though we might need two or more to ensure liveness). It also reduces the amount of stake required for security and encourages setting a faster stake unbonding time (bonded collateral can be withdrawn once the delay period elapses).
\ Furthermore, interoperability protocols based on optimistic verification are described as “inheriting security of the underlying blockchain”; this is based on the idea that if the underlying blockchain is live and not censoring fraud proofs, a malicious relayer cannot get away with dishonest behavior. More, attacking the protocol would require attacking the blockchain itself since censoring transactions for a prolonged period requires controlling a majority of nodes—and by extension, stake/mining power—in the network.
\
\ But even optimistic verification has unique drawbacks. For instance, imposing a delay on finalization and execution of bridging transactions or message requests increases latency and degrades overall user experience. This type of cross-chain security also has several subtle “gotchas” with implications for security, such as the possibility of a malicious party challenging valid transactions to “grief” honest relayers and execute a type of DDoS attack.
\ Since fraud proofs are (mostly) interactive by nature, an invalid challenge would cause honest relayers to waste resources—including funds spent on gas fees for on-chain transactions. Consequently, honest relayers may lose incentive to relay cross-chain information, potentially leaving an opportunity for dishonest relayers to relay cross-chain information. Requiring challengers to post a minimum deposit could deter griefing, but a high minimum deposit could discourage honest watchers (who lack capital) from challenging invalid state updates.
\ Some protocols work around this problem by restricting challenges to a permissioned set of watchers, but that brings us back to the original problem of having a small set of (trusted) participants to secure a system. This approach can also produce several unintended consequences, such as reducing the barrier to collusion among watcher nodes and improving an attacker's chances of corrupting the majority of nodes watching the system.
Cryptographic verificationThe final approach to securing cross-chain interoperability protocols which we’ll consider comes from the realm of cryptographic proofs. The idea is simple: instead of trusting people to verify cross-chain states (which previous sections have shown to be perilous in certain cases), we can instead use cryptographic verification mechanisms—reducing trust assumptions to the minimum.
\ Here, one or more actors generate SNARK (Succinct Non-Interactive Argument of Knowledge) proofs of a chain’s (valid) state for use within an interoperability application. These proofs are verifiable: we can take a cryptographic proof of a cross-chain state, such as one derived from a block header, and confirm its validity. They are also non-interactive: a proof generated by a single party can be verified by n different parties without anyone to communicate (unlike interactive fraud proofs). Interoperability protocols designed this way often have the lowest trust assumptions, insofar as the underlying proof system is sound (i.e., an adversary cannot create valid proofs for invalid claims, except for a negligible probability).
\ Such protocols are also different from externally verified systems, especially where cryptographic proofs verify that each block is correct according to a chain’s consensus protocol. As such, an adversary would need to control a supermajority of the source chain’s validator’s set—required to finalize invalid blocks—to corrupt an interoperability protocol using cryptographic proofs of cross-chain state.
It is also easy to see how this approach eliminates some of the drawbacks associated with some cross-chain security mechanisms discussed previously:
\
Zero capital inefficiency: The use of zkSNARKs to verify cross-chain states eliminates the need for a staking/bonding mechanism and the associated inefficiency of subjecting tokens to a lockup period. Similarly, relayers need not post a bond (unlike optimistic verification) before making claims about cross-chain transactions since the accompanying proof succinctly verifies the claim.
Low latency: Without the need to implement a delay period—to enable timely fraud proofs—an interoperability protocol can execute a cross-chain message or bridging operation once a SNARK proof securing it is verified. That said, proof generation is typically compute-intensive, so an externally verified system may be more efficient compared to a SNARK-based interoperability protocol.
\ When assessing the security of a “cryptographically verified” interoperability solution, it’s important to look closely at what information about cross-chain states is actually being proven and verified. Zero-knowledge proofs have become a buzzword that many protocols have latched on to in order to obfuscate the actual trust assumptions that underlie their protocols.
\ For instance, because verifying all of the signatures across the Ethereum validator set (over 925,000 validators per current figures) in a zkSNARK circuit can be expensive, some protocols have historically adopted other means of deriving proofs of Ethereum’s state. An example is an “Ethereum to X” bridge (where X can be any blockchain) that generates a proof that the block headers were signed by a majority of Ethereum’s Sync Committee (which we introduced earlier).
\ This is a more feasible approach (compared to verifying public keys of thousands of validators that attested to a block). But as explained earlier, validators in the Sync Committee are not slashed for signing off on incorrect block headers—leaving a non-negligible probability that a majority of Sync Committee members can collude or be bribed into deceiving light clients and effectively jeopardizing the security of bridges/messaging protocols relying on the Sync Committee for information.
\ Moreover, as explained in the original article introducing Lagrange State Committees, we explained that, in an ideal world where malicious Sync Committee were liable to slashing, economic security would be capped at the maximum slashable amount. Here are some excerpts from that post for context:
\
The security of light client bridges, ZK bridges and sync committee proofs are all based on verification of signatures from the Ethereum light client sync committee. As the size of the sync committee is fixed, the economic security that underpins it is also capped over a 27-hour window. Once slashing is eventually implemented for Ethereum sync committees, the economic security will be bounded as follows:
- Economic security of Sync Committee = 512 nodes * 32 Eth * $1650 USD/ETH = $27,033,600
- Threshold to compromise Sync Committee = $27,033,600 * 2/3 = $18,022,400
\ While light client bridges and ZK light client bridges are thought of as a gold standard for cross-chain interoperability, the amount of assets they can secure with randomized sync committees is severely limited. As previously shown, the amount of collateral that colluding nodes would have to burn to simultaneously compromise all Ethereum light client and ZK light client bridges is capped at $18m.
\ Consider a situation, where the sum of the value of all assets secured by all light client and ZK light client bridges is of an amount k. When k < $18m, all assets secured across the bridges are safe, as an attack is not economically viable. As k grows such that k > $27m , it becomes profitable for a group of bad actors in the sync committee to attest to malicious blocks in order to compromise the secured assets.
\ We encourage reading the entire article, particularly the section on the limitations of Ethereum’s light client bridges, for more context on the issues around relying on randomized sync committees to derive proofs of cross-chain states. We also suggest that you follow Polyhedra Network’s efforts to prove the full Ethereum PoS consensus in a ZK circuit.
Lagrange State Committees: Shared security-as-a-service for cross-chain communication protocolsWith a major part of this article’s introduction dwelling on shared security, it is only fitting that we introduce a shared security solution we’ve been working on at Lagrange Labs: Lagrange State Committees. In this section, we’ll explore the inner workings of the Lagrange State Committee network and understand its connection to Lagrange’s ZK Big Data stack and the goal of building tools to enable secure and expressive state access on chains and between chains.
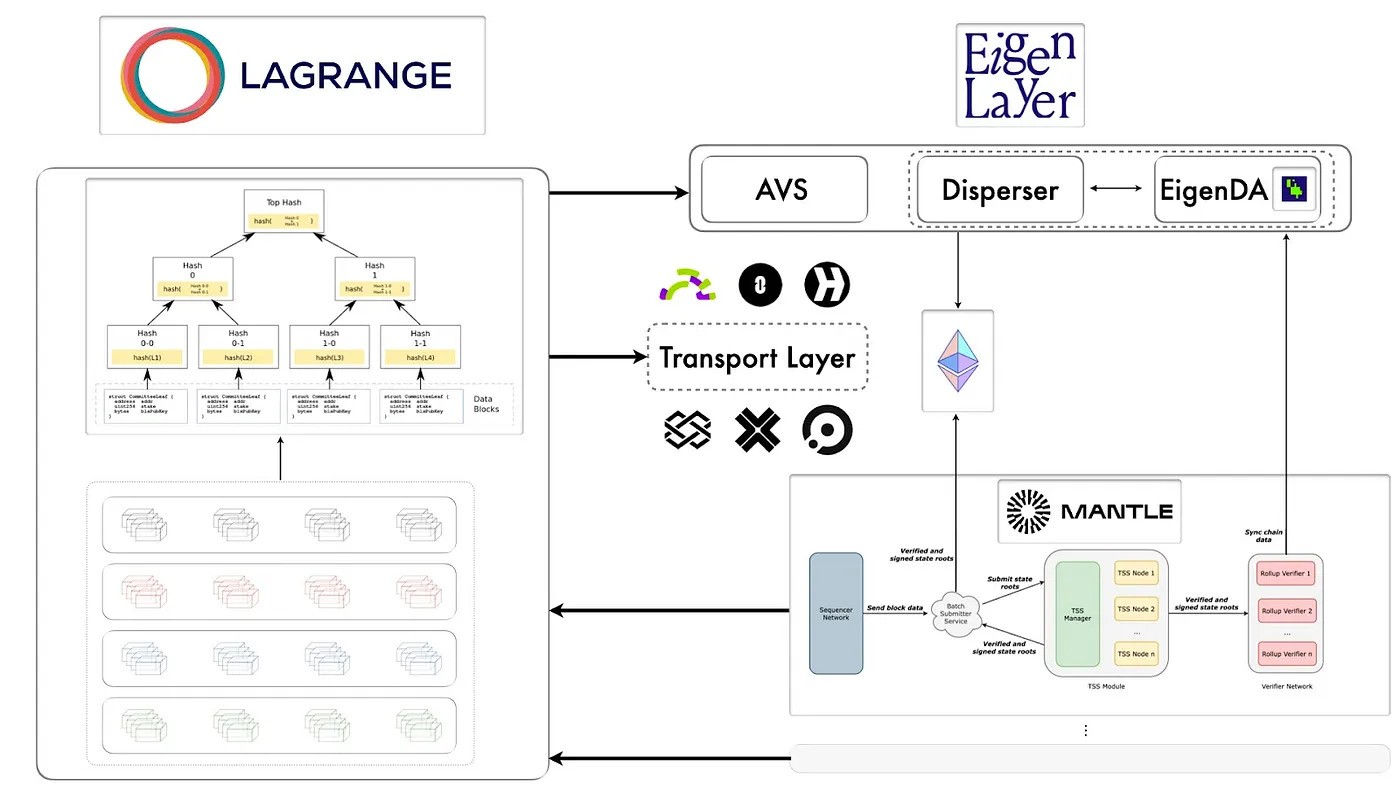
What are Lagrange State Committees?The Lagrange State Committee (LSC) network is a simple and efficient ZK light client protocol for optimistic rollups (ORUs) that settle on Ethereum (e.g., Optimism, Arbitrum, Base, and Mantle). LSCs are conceptually similar to Ethereum’s Sync Committee and support light client-based applications—like bridges and interchain message layers—that want to use an optimistic rollup’s state without taking on excessive trust assumptions.
\ A Lagrange State Committee is a group of client nodes that have restaked 32 ETH worth of collateral on Ethereum via EigenLayer. In other words, a Lagrange State Committee network is an AVS or Actively Validated Service. Each Lagrange State Committee attest to the finality of blocks for a given optimistic rollup once the associated transaction batches are finalized on a data-availability (DA) layer. These attestations are then used to generate state proofs, which applications can treat as a source of truth for the state of that particular optimistic rollup.
\
\ While Ethereum’s Sync Committee is capped at 512 nodes, each Lagrange State Committee network supports an unbounded set of nodes. This ensures that economic security is not artificially capped and the number of nodes attesting to the state of an optimistic roll up can scale, thereby dynamically increasing the economic security behind Lagrange state proofs.
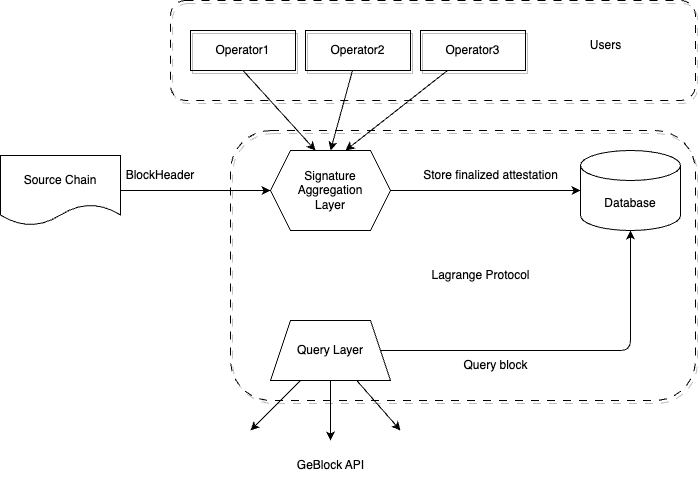
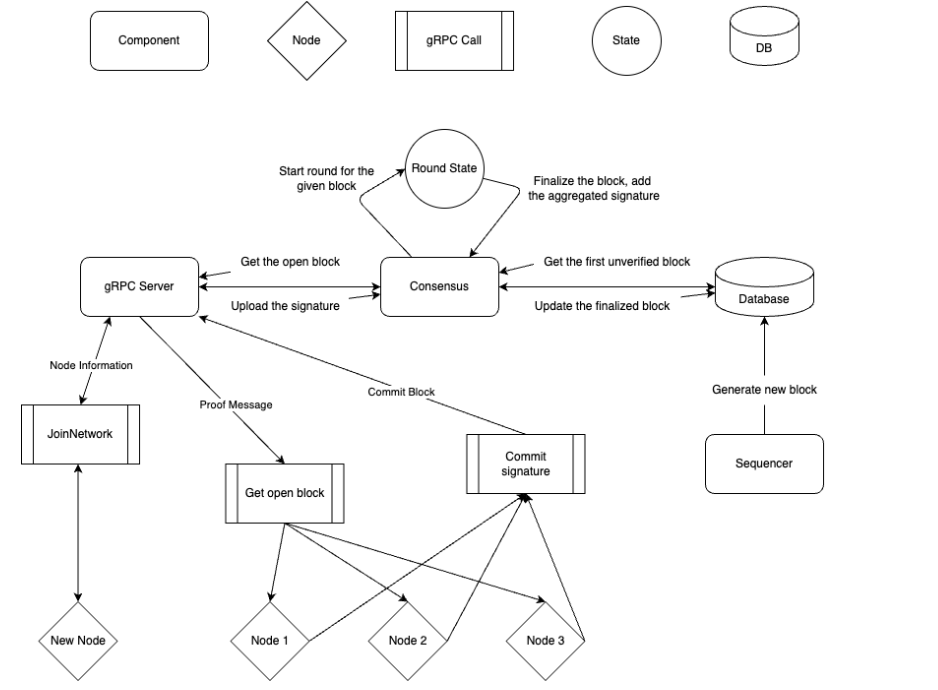
How does the Lagrange State Committee network work?Two key components of the Lagrange State Committee protocol are the sequencer and client nodes (“client nodes” is another name for validators registered to a Lagrange State Committee). The sequencer is a central entity responsible for coordinating attestations in a Lagrange State Committee network and serving attestations to the provers that produce state proofs. The sequencer node is actually a combination of three modules with different functions: Sequencer, Consensus, and Governance.
\ At specific intervals, the Sequencer module requests attestations from client nodes to rollup blocks resulting from the execution of a batch of transactions that were written to a DA layer. Instead of executing this routine for every optimistic rollup block, we Below is a brief analysis of each element in the block message:
\ (1). Block_header: A header of a finalized optimistic rollup (ORU) block. “Finality” here means a block derived by rollup nodes from transaction data finalized on a given DA layer. For example, finality is defined by the safe L2 head for Optimism/OP stack rollups and an L2 block with Ethereum equivalent finality for Arbitrum and Arbitrum Orbit chains. (Learn more about rollup finality in this article.)
\ (2). current_committee: A cryptographic commitment to the set of public keys associated with client nodes permitted to sign a block b. A client node is expected to build a Merkle tree, with leaves representing public keys of all active committee members, and sign the root of the Merkle tree with its BLS12–381 key.
\ (3). next_committee: A cryptographic commitment to the set of public keys associated with nodes permitted to sign the next block (b+1). Nodes that wish to leave a state committee must submit a transaction at the end of the attestation period to the Lagrange Service contract on Ethereum that handles registration and deregistration of operators in the State Committee AVS.
\ At the end of each attestation period, the set of committee nodes may be altered if operators request to leave or join before the next attestation period commences. Client nodes are expected to build a Merkle tree of the next_committee by retrieving the current set of nodes registered to each committee from the Lagrange Service Contract.
ELI5: What are state proofs?A state proof is a cryptographic proof of a blockchain’s state: a proof of a block header from a source chain (chain A), which can be used to prove to the destination chain the existence of a state on the source chain, such as a particular transaction. In other words, a state proof represents a proof of the source chain’s state at a specified block height.
\ To illustrate using a previous example: the block header from the source chain (chain A), which Bob’s application on the destination chain (chain B) uses to verify the existence of Alice bridging transaction, is a state proof. It represents a summary of modifications to the source chain’s state between the previous block and the current block. If Alice’s Merkle proof verifies against the transactions tree root stored in chain A’s block header, Bob can confidently approve the bridging transaction on chain B (the destination chain) as the state proof attests to the execution of Alice’s message request on the origin chain.
\ The Lagrange State Committee network is designed to generate state proofs for optimistic rollups secured by Ethereum. State proofs are generated by aggregating BL12–381 signatures on the tuple described earlier (block_header, prev_committee, and next_committee) from at least two-thirds of nodes in the state committee. The state proof is then generated by a SNARK circuit based on the collective weight of signatures attesting to a given block header.
\
\ The approach of requiring attestors to commit to the current and next state committees is similar to the Ethereum Sync Committee protocol and achieves a similar goal: enabling light clients to verify the validity of an optimistic rollup block header efficiently and securely. Each state proof is cryptographically linked by a series of next_committee commitments indicating which nodes should sign the next block. Thus it is enough to verify a SNARK proof that proves the following recursive properties in the block object signed by attesting nodes:
\
At least ⅔ of the n nodes in the state committee signed the block header b.
The current_committee of block b equals the next_committee tree of block b-1.
Block b-1 is either the genesis block, or is valid with respect to these three conditions.
\
Interoperability protocols and other applications that require secure optimistic rollup state with fast finality (e.g., cross-chain bridges and messaging protocols) can use state proofs from Lagrange State Committees with minimal trust assumptions. Importantly, the Lagrange State Committee network is able to guarantee security of state proofs by implementing deterministic slashing of malicious attestors and inductive validity proofs.
How does the Lagrange State Committee network interoperate with the ZK Big Data Stack?In the first post of the series on Lagrange’s product suite, we highlighted the relationship between different parts of the ZK Big Data Stack: Lagrange State Committees, Recproofs, zkMapReduce, and the Lagrange Coprocessor. Each of these components, when combined together, collectively provide secure, efficient access to state and expressive, dynamic computation on state data:
\
#1. The Lagrange State Committee network integrates with the other components of the ZK Big Data Stack for better performanceWe use Recproofs and zkMapReduce to create updatable aggregate public key (APK) proofs for state committees—allowing us to avoid the costly and time-consuming process of deaggregating and re-aggregating public keys of non-signers whenever a new aggregate signature has to be created created.
\ Efficient aggregation of BLS public keys of operators in the Lagrange State Committees AVS facilitates higher participation rates in the AVS without increasing computational cost of verifying attestations from state committee nodes. This is why Lagrange State Committees are able to support a potentially unbounded set of nodes and exhibit superlinear security as more capital is pooled into state committees. You can learn more about this property in our post on scaling programmable trust on EigenLayer with ZK Big Data.
\ Integrating Lagrange State Committees with the ZK Big Data stack also has more direct benefits for client applications leveraging Lagrange state proofs. For example, we can use the Lagrange Coprocessor’s zkMapReduce feature to combine multiple state proofs from n optimistic rollup chains into a single multi-chain state proof. This allows for “nested verification”, where a single on-chain transaction simultaneously verifies the state of multiple optimistic rollups, and reduces verification costs for client services.
\
#2: The Lagrange Coprocessor integrates with the Lagrange State Committee network to power trustless off-chain computationThe Lagrange Coprocessor—which we will analyze extensively in a subsequent post—supports cheap and scalable computation on on-chain data by performing computations off-chain. Cross-chain interoperability protocols who integrate with the Lagrange State Committees can also integrate with the Lagrange Coprocessor, to facilitate expanding their cross-chain offerings to include verifiable computation.
\ For instance, a developer building a multi-chain lending application may want to calculate the sum of collateral deposited by a user across n different rollups. Our friendly developer can leverage the Lagrange Coprocessor to compute this value, using whatever block header source the cross-chain protocol already relies on.
Why Lagrange’s State Committees network is a game-changer for interoperability in optimistic rollups Shared, superlinear security for optimistic rollup light clientsCurrently, interoperability protocols that support bridging between optimistic rollup chains are independently responsible for verifying the state of source chains. The security of these interoperability protocols depends on the mechanism for verifying that a block header is correct.
\ Some cross-chain communication protocols attempt to reduce trust assumptions by implementing native staking and asking a set of verifiers to bond collateral before attesting to block headers of source chains. However, this fragments economic security across different cross-chain protocols, as the cost of corrupting a subset (k of n) of each protocol’s validator set is lower.
\ In contrast, Lagrange State Committees allow multiple cross-chain protocols to derive security from a single, dynamic set of validators that can scale to an unbounded size. This changes the status quo—where each interoperability protocol is independently responsible for verifying the accuracy of cross-chain states—to one where multiple applications can consume cross-chain state from a single source.
\ Unlike other light client protocols, Lagrange’s State Committee network supports a dynamic, unbounded set of attesting nodes. The economic weight of signatures securing each attestation can, therefore, scale dynamically as more stake is pooled into the state committees—enabling a superlinear increase in security and raising the difficulty of attacking integrated cross-chain protocols in isolation.
\
\ This effectively makes the Lagrange State Committee a “shared security zone” that any cross-chain protocol (regardless of its size) can plug into for maximum security—similar to how the Relay Chain on Polkadot and Cosmos Hub on Cosmos secure secondary networks in the multichain ecosystem. Additionally, integrating with EigenLayer’s restaking middleware enables the Lagrange State Committee network to extend Ethereum’s economic security to secure an arbitrary number of downstream cross-chain communication protocols.
Reduced overhead for cross-chain product development teamsA developer building a cross-chain interoperability protocol today must develop infrastructure to independently run watchers to verify the state of every optimistic rollup that they support. As the number of integrated optimistic rollups grow, the infrastructure overhead of managing security across each origin chain increases.
\ Integrating with the Lagrange State Committee allows the developer to outsource their security and instead focus resources on optimizing their product features. To put this into context: Each Lagrange state proof is lightweight enough to be verified efficiently on any EVM compatible chain.
Additional security for existing interoperability protocolsLagrange state proofs are agnostic to the transport layer used to transport them to the one or more destination chains, allowing interoperability applications to seamlessly stack Lagrange state proofs with existing security mechanisms. For example, a cross-chain oracle or cross-chain messaging protocol with an independent verifier set can verify a Lagrange state proof as an added security measure before relaying cross-chain message requests from optimistic rollups.
\ Moreover, an existing interoperability protocol—once integrated with the Lagrange State Committee network—can add support for optimistic rollups without requiring validators to increase the number of chains they monitor. By using state proofs from the Lagrange State Committee network, validators only have to relay message requests between rollups. A gateway contract on the destination chain can then validate the existence of messages passed by relayers by verifying a Lagrange state proof.
How does the Lagrange State Committee network compare to other cross-chain security mechanisms?Lagrange State Committees compare favorably to existing interoperability infrastructure that utilize bonded staking/slashing, permissioned validation, and optimistic verification mechanisms (among others) to enhance security of cross-chain state proofs. Below are some comparisons:
External verification by permissionless validatorsLagrange’s restaking model mitigates a key problem in cross-chain security mechanisms that implement pure PoS staking for security: risk stacking. Take, for example, a cross-chain protocol that requires validators to buy and lock up a protocol’s native token for the bonding period. As the popularity of the cross-chain protocol’s native token changes, the volatility of the asset’s price affects the total economic security of the network.
\ Price volatility is less of a problem for the Lagrange State Committee network as the security of committee nodes is based on restaked collateral through EigenLayer. In addition, restaked collateral has reduced opportunity costs for prospective validators, meaning more participation in state committees and a higher level of economic security for interoperability protocols. For users, this means lower fees and more security compared to interoperability protocols that independently bootstrap their security.
\ We also note that consensus protocols used in traditional Proof-of-Stake place limitations on validator count (e.g., Tendermint BFT caps participation at 100-200 validators) and prevent traditional PoS protocols from scaling economic security as often as needed. Conversely, the Lagrange State Committee network uses an attestation mechanism that supports a potentially unbounded set of nodes participating in consensus. This ensures that the network can dynamically increase the number of attestors and by extension, provide more robust guarantees of economic security for client applications.
External verification by permissioned validatorsProof-of-Authority (PoA) based cross-chain protocols rely on attestations to block headers from a small set of permissioned nodes. These approaches have historically proven insecure with high profile incidents including the Ronin hack (5 out of 7 validators compromised) and Harmony One bridge hack (2 out of 5 validators compromised).
\ Using a permissionlessly validated system like the Lagrange State Committee network does reduce efficiency somewhat compared to a centralized operator or validator set signing headers. But given the amount at risk, we consider this a sensible tradeoff. Permissionlessly validated systems also decrease the attack surface for companies who, more often than not, may end up running a majority of validators in a permissioned system.
Canonical bridgingThe Lagrange State Committee network eliminates the latency of sending cross-chain messages from optimistic rollups. Each LSC acts as a “fast mode” for bridges and messaging protocols whose users would like to bridge from an optimistic rollup without waiting out the challenge window. Optimistic rollups also directly benefit from the LSC’s fast-finality property as it solves a key UX pain point for L2 users.
\ This guarantee derives from the observation that: (a) the slashing mechanism is designed to raise the cost of adversarial actions, and (b) slashing of colluding nodes in a LSC can happen on-chain in slow mode as there is variable time delay on withdrawal of stake. In summary, participants in a LSC always have the incentive to attest to correct cross-chain states—which enables cross-chain applications to use state proofs from an LSC immediately and with minimal trust assumptions backed by the rollup’s canonical bridge.
ConclusionThis article has covered quite a lot of ground, and we hope reading it has been educational—if not valuable—for builders, investors, enthusiasts, and users in the interoperability space. Over the course of this article, we've explored the definition of shared security, what it means for designing secure protocols, and how cross-chain interoperability can benefit from integrating with shared security infrastructure.
\ We've also explored Lagrange State Committees: our shared security-as-a-service solution designed with cross-chain communication protocols in mind. Lagrange State Committees is part of our vision of enabling secure, trust-minimized, and efficient interoperability and will be part of a larger stack enabling developers to build powerful cross-chain applications for users.
\ The multichain future is inevitable and it is important that users can go from using one chain to 10000s of chains without experiencing significant loss of security. Solutions like Lagrange State Committees (along with other advancements in cross-chain security) are critical to this goal. With interoperability receiving more attention than ever, a world where moving across chains is secure and efficient is very well within reach of crypto users around the world.
AcknowledgementsEmmanuel Awosika (2077 Research), Omar Yehia (Lagrange Labs), Ismael Hishon-Rezaizadeh (Lagrange Labs), and Amir Rezaizadeh (Lagrange Labs) contributed to this article. Emmanuel was contracted by Lagrange Labs to support the writing of this article.
\ A version of this article was previously published here.
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.