and the distribution of digital products.
A Guide to Naming and Mapping Monographs
:::info Author:
(1) Thierry Boy de la Tour, Univ. Grenoble Alpes, CNRS, Grenoble INP, LIG 38000 Grenoble, France.
:::
Table of Links2 Basic Definitions and Notations
2.3 Signatures and Algebras and 2.4 Categories
3 Monographs and their Morphisms
6 Graph Structures and Typed Monographs
7 Submonographs and Partial Morphisms
8 Algebraic Transformations of Monographs
5 Drawing Monographs
\ It is sometimes necessary to name the edges in a drawing. We may then adopt the convention sometimes used for drawing diagrams in a category: the bullets are replaced by the names of the corresponding nodes, and arrows are interrupted to write their name at a place free from crossing, as in
\

\ Note that no confusion is possible between the names of nodes and those of other edges, e.g., in
\
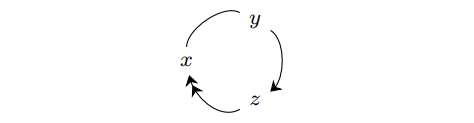
\ it is clear that x and z are nodes since arrow tips point to them, and that y is the name of an edge of length 3.
\

\ One particularity of monographs is that edges can be adjacent to themselves, as in
\
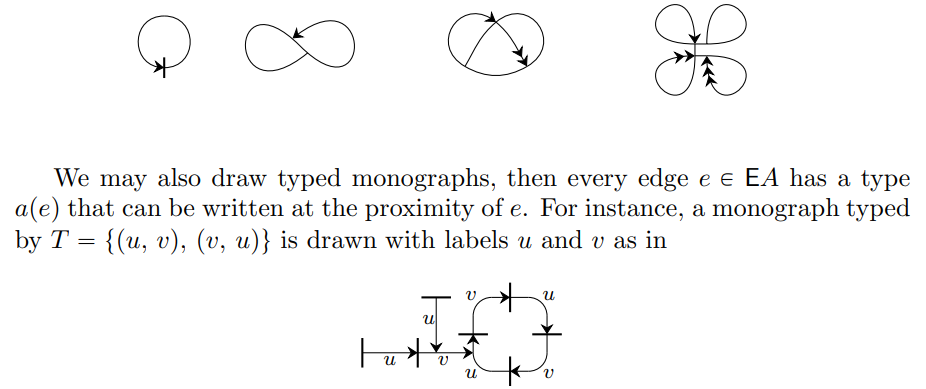
\ Of course, knowing that a is a morphism sometimes allows to deduce the type of an edge, possibly from the types of adjacent edges. In the present case, indicating a single type would have been enough to deduce all the others.
\ In particular applications it may be convenient to adopt completely different ways of drawing (typed) monographs.
\

\
6 Graph Structures and Typed Monographs\

\
\
\

\
\
\

\ \ The next lemma is central as it shows that no graph structure is omitted by the functor S if we allow sort-preserving isomorphisms of graph structures. We assume the Axiom of Choice through its equivalent formulation known as the Numeration Theorem [5].
\
\

\
\
\

\ \ It is therefore clear that if S were full it would be an equivalence of categories, but this is not the case as we now illustrate on graphs.
\

\
\
\

\
\
\
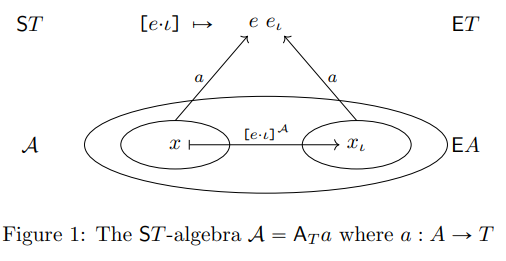
\ \ The type indicated by the syntax (and consistent with the drawings of E-graphs in [2]) is of course T1.
\
\

\
\
\

\
\
\
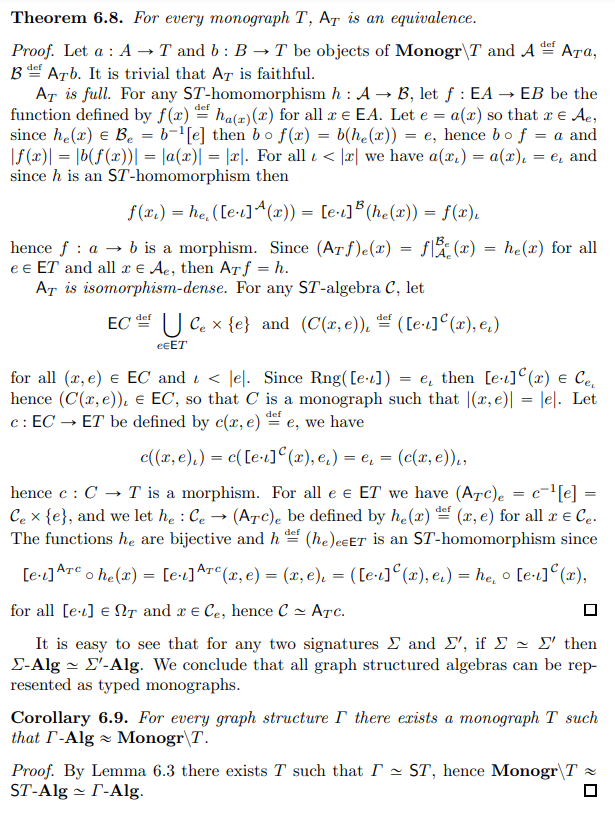
\
\
\

\
\
\

\ \
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright 2025, Central Coast Communications, Inc.