and the distribution of digital products.
DM Television
A Formalization of the SylloBio-NLI Resource Generation Process
-
\
A. Formalization of the SylloBio-NLI Resource Generation Process
B. Formalization of Tasks 1 and 2
C. Dictionary of gene and pathway membership
D. Domain-specific pipeline for creating NL instances and E Accessing LLMs
H. Prompting LLMs - Zero-shot prompts
I. Prompting LLMs - Few-shot prompts
J. Results: Misaligned Instruction-Response
K. Results: Ambiguous Impact of Distractors on Reasoning
L. Results: Models Prioritize Contextual Knowledge Over Background Knowledge
M Supplementary Figures and N Supplementary Tables
A Formalization of the SylloBio-NLI Resource Generation ProcessThis appendix formalises the generation process of the syllogistic inference patterns.
\ We start by defining the mains constructs (formal and linguistic artefacts and functions) of the underlying framework:
\
Syllogistic Scheme (S): A logical inference pattern consisting of premises and a conclusion, S = {P1, P2, . . . , Pn, C}, where Pi is premise i and C is the conclusion.
\
Formal Argument Scheme (σ): Representation of a syllogistic scheme in first-order logic (FOL), σ(S) = {ϕ1, ϕ2, . . . , ϕn, ψ}, where ϕi corresponds to Pi and ψ corresponds to C.
\
Natural Language Template (τ ): A natural language schema mapping each formula in σ(S) to a sentence template, τ (σ(S)) = {τ1, τ2, . . . , τn, σ}, where τi is the sentence template for ϕi and σ is the sentence template for ψ.
\
Ontology (O): A domain-specific knowledge base containing entities E and predicates Π, O = {E, Π}, where E = {e1, e2, . . . , ek} and Π = {π1, π2, . . . , πl}.
\
Instantiation Function (I): A function that replaces placeholders in τ with entities and predicates from O, I : τ (σ(S)) × O → NL, where NL is the set of natural language sentences.
\
Expert Mapping Function (µExpert): A function provided by a domain expert to map placeholders to appropriate ontology terms, µExpert : Placeholders → E ∪ Π.
\
Knowledge Base (KB): A collection of instantiated syllogistic arguments, KB = {A1, A2, . . . , Am}, where Ai = {P ′ 1 , P′ 2 , . . . , P′ n , C′} and P ′ i , C′ are instantiated natural language sentences.
The process formalisation defines a systematic process for generating domain-specific syllogistic arguments by:
\ 1. Defining formal representations of syllogistic schemes in first-order logic.
\
Generating natural language templates from these formal representations.
\
Mapping placeholders to domain-specific entities and predicates using an ontology and expert knowledge.
\
Instantiating the templates to produce logically valid and semantically sound arguments.
\
Constructing a knowledge base for evaluating NLI models.
\ This ensures that the generated arguments are both logically valid and contextually relevant to the biomedical domain.
\ Input: A set of syllogistic schemes: S = {S1, S2, . . . , Sm}, an ontology: O = {E, Π}, an expert mapping function: µExpert.
\ Output: A knowledge base of instantiated arguments: KB.
\ Step 1: Formal Argument Scheme Selection: For each syllogistic scheme Si ∈ S, define its formal argument scheme in first-order logic:
\
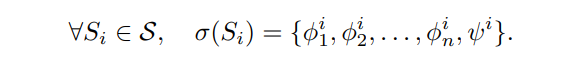
\ Step 2: Natural Language Template Generation: Transform each formula in σ(Si) into a natural language template:
\
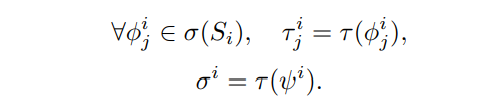
\ Step 3: Ontology Mapping and Instantiation: Apply the expert mapping function to select appropriate entities and predicates from the ontology:
\
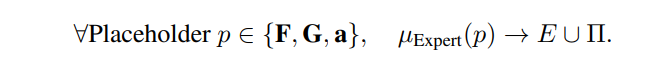
\ Instantiate the templates:
\
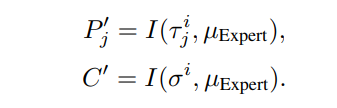
\ under the following constraints:
\ • Logical Validity: The instantiated arguments must preserve the logical structure of σ(Si).
\ • Domain Soundness: The selected entities and predicates must be semantically coherent within the targeted subdomain.
\ These constraints can be further formalised as:
\ Logical Validity Constraint: The instantiated argument Ai must be logically valid:
\ {ϕ ′ 1 , ϕ′ 2 , . . . , ϕ′ n} |= ψ ′ ,
\ where ϕ ′ j corresponds to the logical form of P ′ j .
\ Domain Soundness Constraint: The entities and predicates used must be semantically valid within the domain:
\ ∀e ∈ E ′ , π ∈ Π ′ , DomainValid(e, π) = True,
\ where E′ ⊆ E and Π′ ⊆ Π are entities and predicates used in Ai
\ Verification of Logical Validity: Ensure that the instantiated premises logically entail the conclusion:
\ {ϕ ′ 1 , ϕ′ 2 , . . . , ϕ′ n} |= ψ ′ ,
\ using logical inference rules.
\ Verification of Domain Soundness: Confirm that:
\ • All entities and predicates are correctly used.
\ • There are no semantic contradictions.
\ Step 4: Knowledge Base Construction: Aggregate all instantiated arguments into the knowledge base:
\
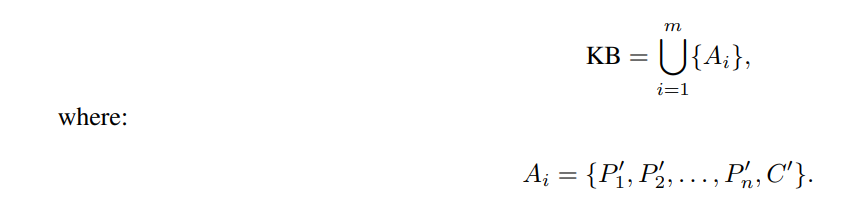
\ This is summarised with the following algorithmic outline:
\

\
:::info Authors:
(1) Magdalena Wysocka, National Biomarker Centre, CRUK-MI, Univ. of Manchester, United Kingdom;
(2) Danilo S. Carvalho, National Biomarker Centre, CRUK-MI, Univ. of Manchester, United Kingdom and Department of Computer Science, Univ. of Manchester, United Kingdom;
(3) Oskar Wysocki, National Biomarker Centre, CRUK-MI, Univ. of Manchester, United Kingdom and ited Kingdom 3 I;
(4) Marco Valentino, Idiap Research Institute, Switzerland;
(5) André Freitas, National Biomarker Centre, CRUK-MI, Univ. of Manchester, United Kingdom, Department of Computer Science, Univ. of Manchester, United Kingdom and Idiap Research Institute, Switzerland.
:::
:::info This paper is available on arxiv under CC BY-NC-SA 4.0 license.
:::
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright 2025, Central Coast Communications, Inc.