and the distribution of digital products.
Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proofs of Auxiliary Lemmas
1.2 Some remarks on dynamics and initial condition
2.1 Establishing the LDP for the SID
2.2 Results related to the LDP
3.3 Proofs of auxiliary lemmas
4 Generalization and References
3.3 Proofs of auxiliary lemmas 3.3.1 Proof of Lemma 3.1: Initial descent to the point of attraction
\
\
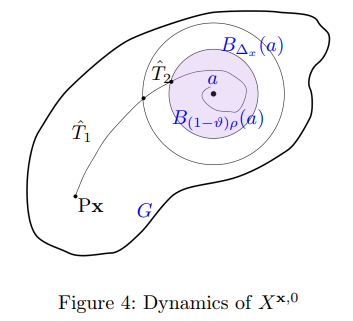
\ Then, by Grönwall’s inequality:
\
\
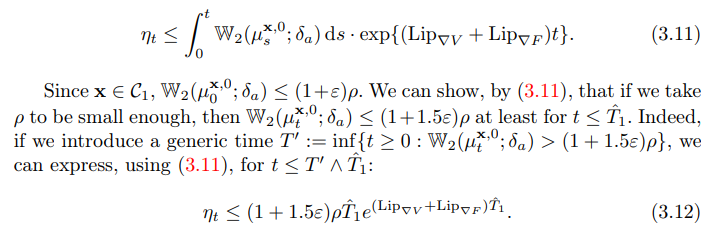
\ That guarantees exponentially fast convergence towards 0:
\
\
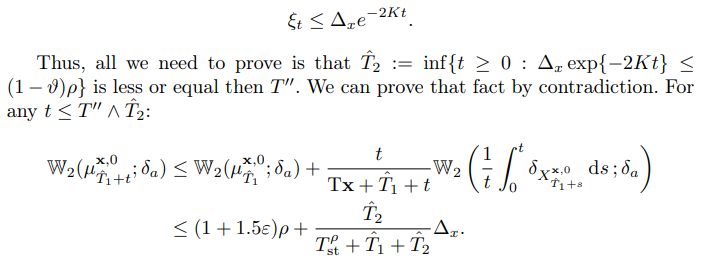
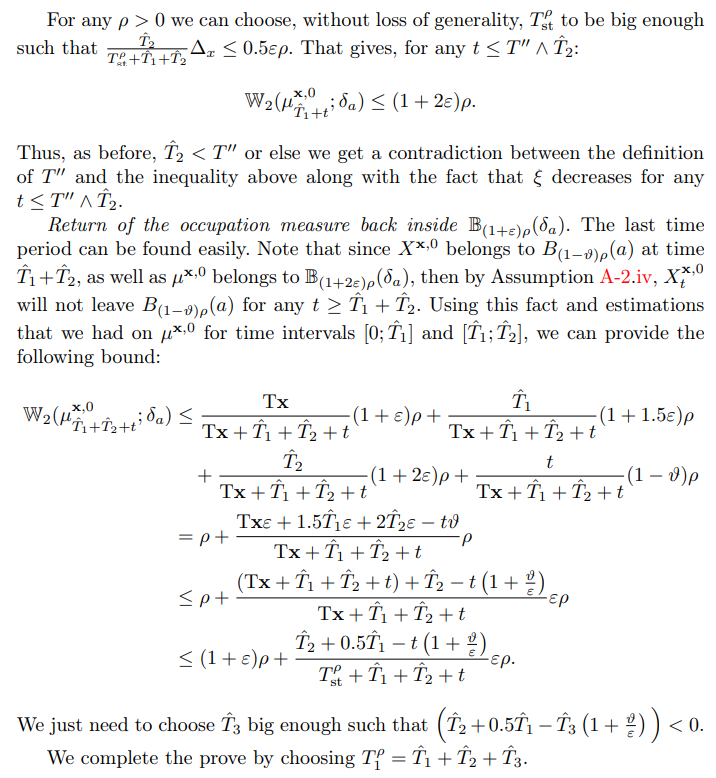
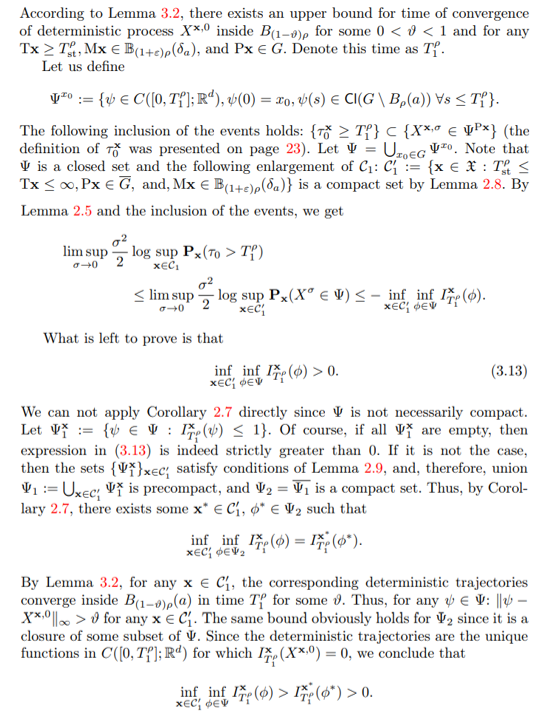
\ And this concludes the proof of the lemma.
3.3.4 Proof of Lemma 3.4: Behaviour in the annulus between Bρ(a) and ∂G
\
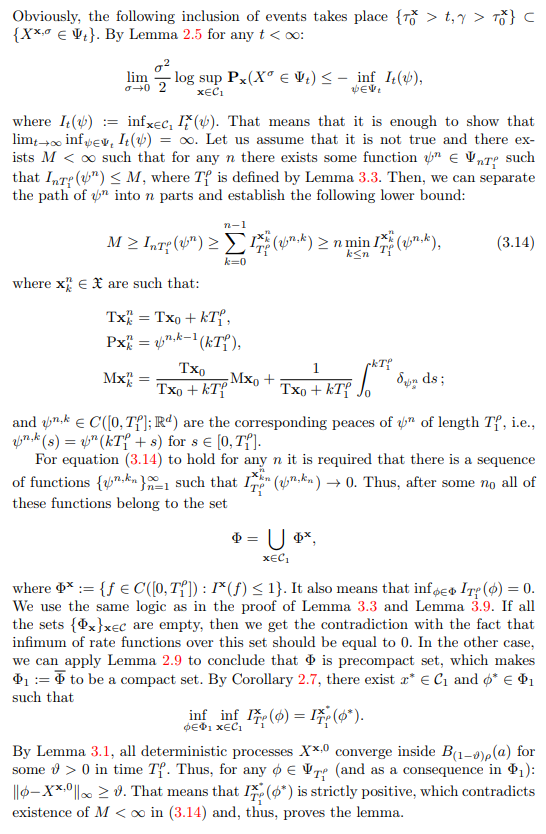
\ Proof. The proof of the following lemma follow the same logic as the one of Lemma 3.3.
\
\ We have to show now that
\
\ This completes the proof.
\ Now we are ready to prove Lemma 3.5 itself.
\
\ That gives us:
\
\
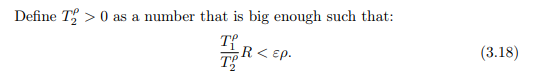
\ We recall that Lemma 3.9 establishes the following asymptotic behaviour for small σ:
\
\
\ Let us first deal with the term B. By (3.22), we have
\
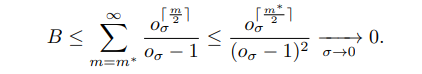
\ Consider now A. Separate each probability inside the sum the following way
\
\
First, we show that it is possible to establish a lower bound for
\
\
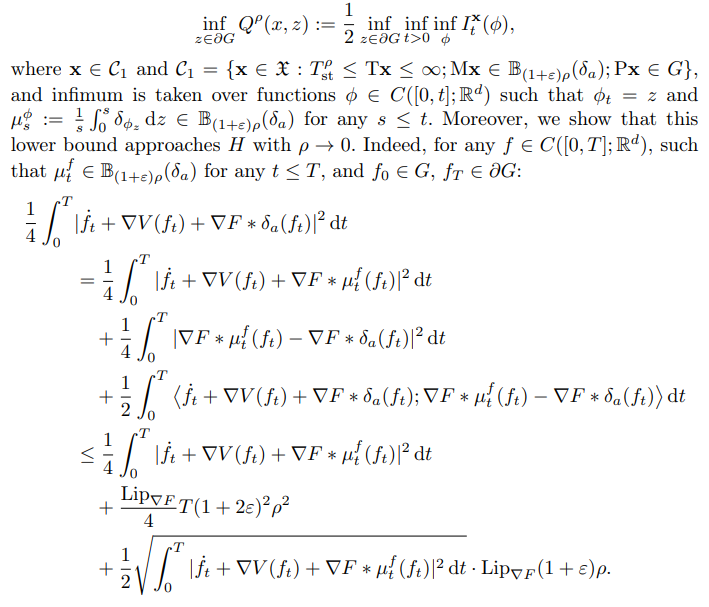
\ By Lemma 2.5,
\
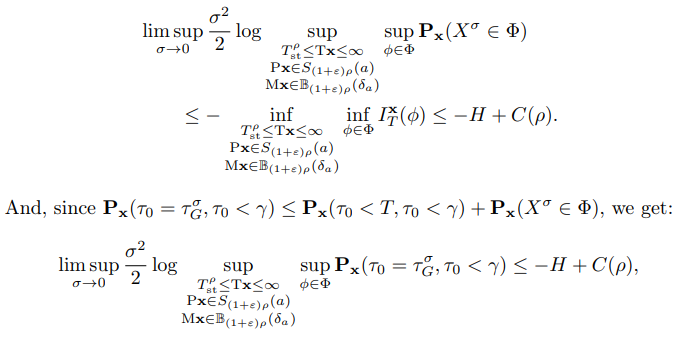
\ which proves the lemma by taking ρ → 0.
3.3.7 Proof of Lemma 3.7: Control of dynamics for small time intervals
\ Use the Jensen’s inequality, integrate the second part of the last integral over s, and get:
\
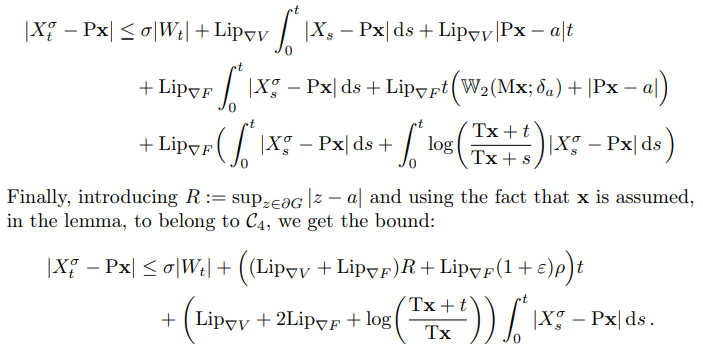
\ We apply Grönwall’s inequality and get:
\
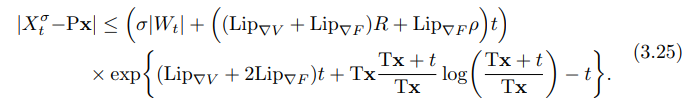
\ Thus, it follows that, for the absolute value of the Brownian motion itself,
\
\
\ Taking into account these remarks, we can now use the Schilder theorem [DZ10, Lemma 5.2.1] that provides the LDP for the path of the Brownian motion. Hence, for some fixed ϵ and 0 < T < 1:
\
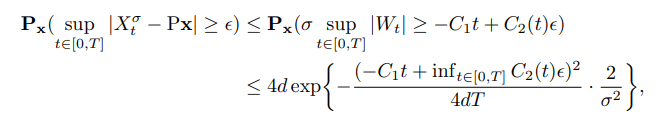
\ where d is the dimension of the space.
\ Note that for any ϵ > 0 the following limit holds:
\
\
\
\
\
\
\
\
\
\
\
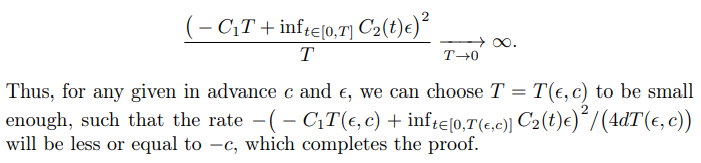
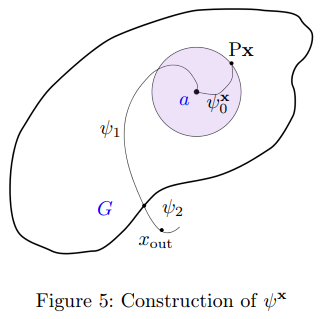
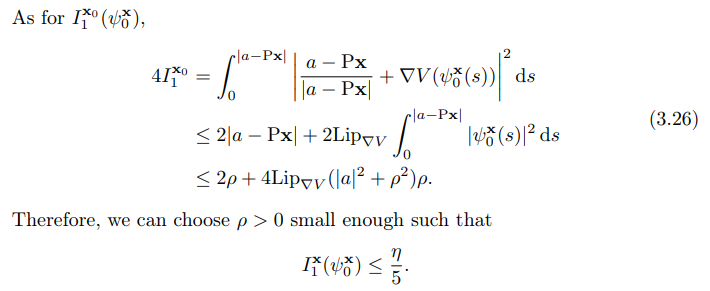
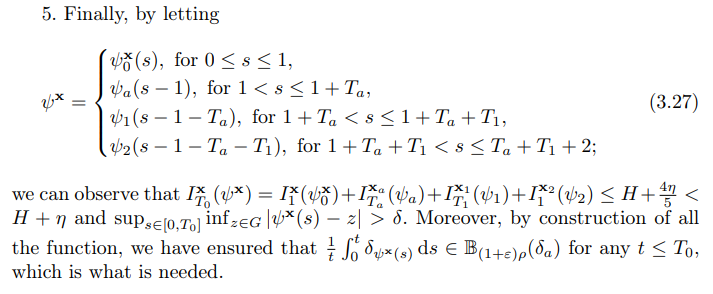
:::info This paper is available on arxiv under CC BY-SA 4.0 DEED license.
:::
:::info Authors:
(1) Ashot Aleksian, Université Jean Monnet, Institut Camille Jordan, 23, rue du docteur Paul Michelon, CS 82301, 42023 Saint-Étienne Cedex 2, France;
(2) Aline Kurtzmann, Université de Lorraine, CNRS, Institut Elie Cartan de Lorraine UMR 7502, Vandoeuvre-lès-Nancy, F-54506, France;
(3) Julian Tugaut, Université Jean Monnet, Institut Camille Jordan, 23, rue du docteur Paul Michelon, CS 82301, 42023 Saint-Étienne Cedex 2, France.
:::
\