and the distribution of digital products.
The Cost of Quantum Bitcoin Mining
C. Comparison with Related Works
II. Background
C. Assumptions and Approximations
IV. Results
V. Discussion, Acknowledgments, and References
B. Performance Measures1. Effective Hash Rate
\ The probability the quantum miner succeeds P easily translates into an effective hash rate. We define the quantum miner’s effective hash rate to be the hash rate of a classical computer which successfully mines the same proportion of blocks. As D is the average number of classical hashes required to mine one block and λ0 := 1/10 minutes is the average time for a block to be mined, the total hash rate of the network is given by Dλ0. The effective hash rate of the quantum miner is then simply
\
\ as P is the expected fraction of blocks the quantum miner adds to the blockchain. Note that this definition for effective hash rate is different from the one in [4].
\ 2. Efficiency
\ Now we analyze the efficiency advantage a quantum computer provides in mining Bitcoin. On average the quantum miner applies mr/λ0 Grover iterations for each block added to the blockchain (by any miner) since the quantum miner is continually applying m Grover iterations in parallel at a rate r and each block takes λ0 average time to be mined. The quantum miner adds P portion of these blocks. Thus, the expected number of Grover iterations applied for each block the quantum miner adds to the blockchain is
\
\ Let Q$ be the cost, in dollars, to implement one Grover iteration. This cost, like the cost of classical mining, is primarily derived from energy expenditures. The expected cost per block for the quantum miner is then
\
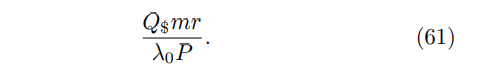
\ Now compare this mining efficiency with that of a classical miner. Let C$ be the cost in dollars to implement one hash on a classical computer. The probability that a single hash yields a marked header is 1/D, so we expect the classical miner to use D hashes per block they mine. Therefore, the expected efficiency for the classical miner is
\
\ and the condition for the quantum miner to be more efficient at mining than a classical miner is then
\
\
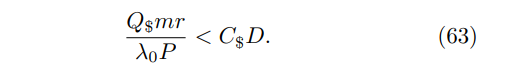
\ We now extend our K <<√D assumption to mK<<√D. As, for the optimal quantum miner, mK = my0r/λ, this extended assumption implies mr/λ <<√D. Taking the first term from the Taylor series expansion of x/(a+x) about x = 0 gives
\
\ where the units of r are Grover iterations per second.
\ The expectation is that as quantum computers improve the cost Q$ of a Grover iteration decreases, and the rate of Grover iterations r increases over time, potentially making quantum mining viable in future. By projecting values of r, Q$, and C$ into the future, estimates can be made for when quantum mining will become advantegous. While we do not compute these projections ourselves, in the next section we evaluate the energy efficiency a quantum computer would require for advantageous mining using the current cost of classical hashes C$ and optimistic assumptions for r.
\
:::info Authors:
(1) Robert R. Nerem, Institute for Quantum Science and Technology, University of Calgary, Alberta T2N 1N4, Canada ([email protected]);
(2) Daya R. Gaur, Department of Mathematics and Computer Science, University of Lethbridge, Alberta T1K 3M4, Canada.
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\