and the distribution of digital products.
Continual Learning RL Agents Set New Standard for Realistic Market Simulations
\
:::tip This is Part 9 of a 11-part series based on the research paper “Reinforcement Learning In Agent-based Market Simulation: Unveiling Realistic Stylized Facts And Behavior”. Use the table of links below to navigate to the next part.
:::
Table of LinksPart 1: Abstract & Introduction
Part 4: Agents & Simulation Details
Part 8: Market and Agent Responsiveness to External Events
Part 9: Conclusion & References
Part 10: Additional Simulation Results
Part 11: Simulation Configuration
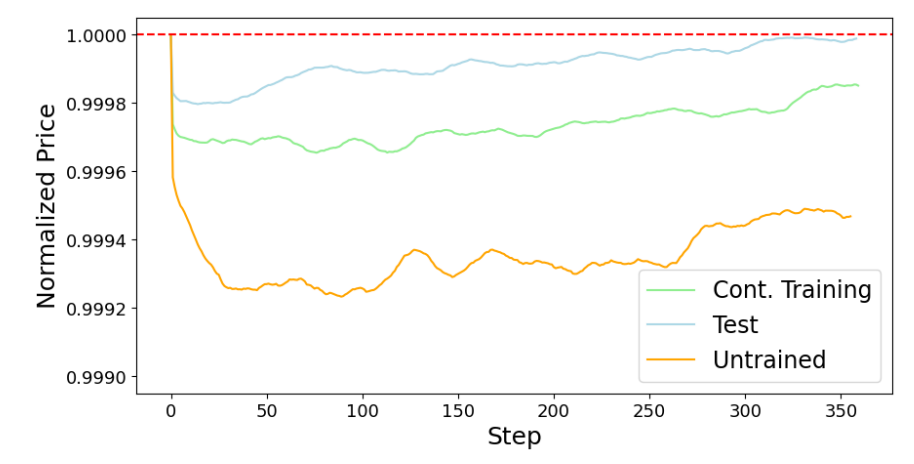
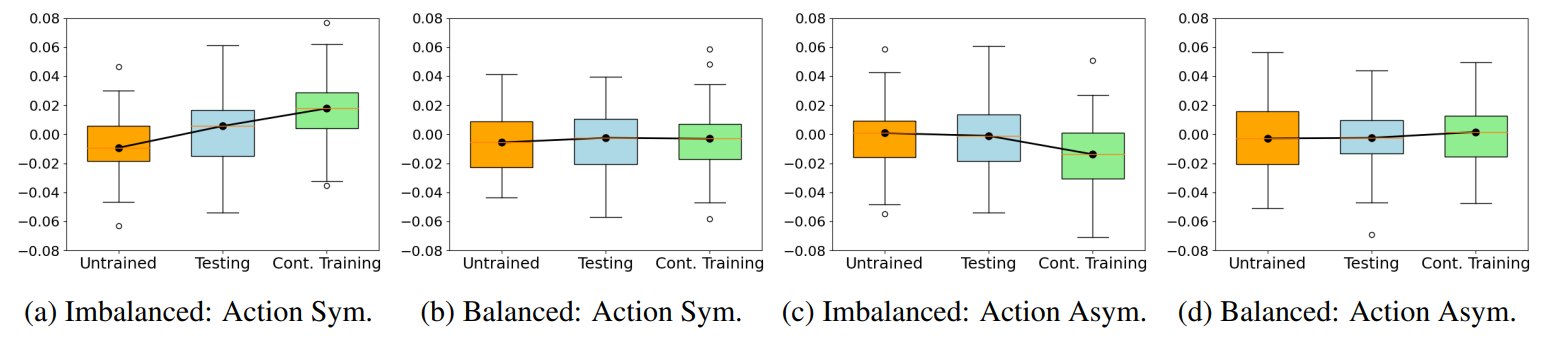
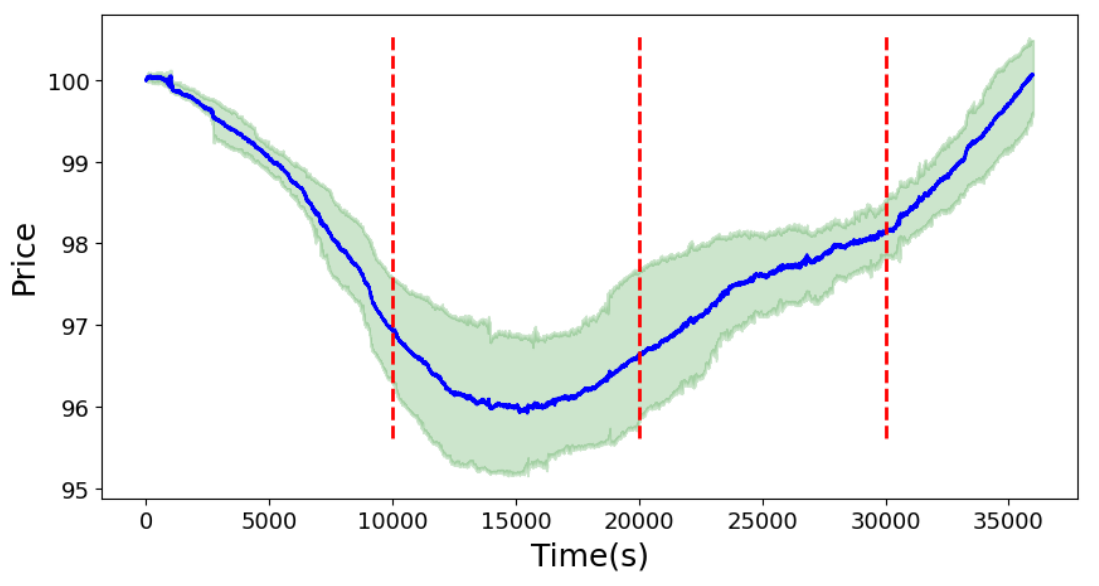
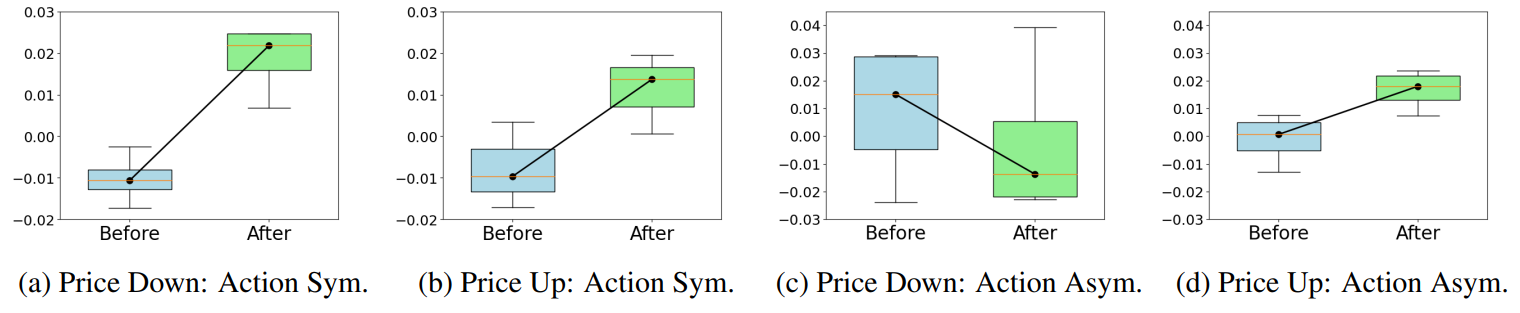
6. ConclusionIn this work, we modify the formulation of RL agents in [6] and implement a highly realistic simulation platform. We compare the simulation results against a real data set and a market simulated using zero intelligence (ZI) traders. The results obtained using the simulation platform show realistic market characteristics and responsiveness to external factors. We find that continual learning RL agents produce the most realistic market simulation, and are capable of adapting to changing market conditions.
\
\
\ Calibration of an agent-based system is still a challenging problem. Vadori et al. [29] and Lussange et al. [7] show two-step procedures to calibrate the RL-based multi-agent system. However, applying these algorithms to our system is very challenging as our system is non-stationary and runs in real time. We plan to address this and other issues in future work.
\
\
[1] R. Cont, “Empirical properties of asset returns: stylized facts and statistical issues,” Quantitative finance, vol. 1, no. 2, p. 223, 2001.
\ [2] R. Cont, S. Stoikov, and R. Talreja, “A stochastic model for order book dynamics,” Operations research, vol. 58, no. 3, pp. 549–563, 2010.
\ [3] I. Ro¸su, “A dynamic model of the limit order book,” The Review of Financial Studies, vol. 22, no. 11, pp. 4601–4641, 2009.
\ [4] M. Raberto, S. Cincotti, S. M. Focardi, and M. Marchesi, “Agent-based simulation of a financial market,” Physica A: Statistical Mechanics and its Applications, vol. 299, no. 1-2, pp. 319–327, 2001.
\ [5] O. Streltchenko, Y. Yesha, and T. Finin, “Multi-agent simulation of financial markets,” Formal modelling in electronic commerce, pp. 393–419, 2005.
\ [6] L. Ardon, N. Vadori, T. Spooner, M. Xu, J. Vann, and S. Ganesh, “Towards a fully rl-based market simulator,” in Proceedings of the Second ACM International Conference on AI in Finance, 2021, pp. 1–9.
\ [7] J. Lussange, I. Lazarevich, S. Bourgeois-Gironde, S. Palminteri, and B. Gutkin, “Modelling stock markets by multi-agent reinforcement learning,” Computational Economics, vol. 57, pp. 113–147, 2021.
\ [8] M. P. Wellman and E. Wah, “Strategic agent-based modeling of financial markets,” RSF: The Russell Sage Foundation Journal of the Social Sciences, vol. 3, no. 1, pp. 104–119, 2017.
\ [9] J. D. Farmer, P. Patelli, and I. I. Zovko, “The predictive power of zero intelligence in financial markets,” Proceedings of the National Academy of Sciences, vol. 102, no. 6, pp. 2254–2259, 2005.
\ [10] J. Moody, L. Wu, Y. Liao, and M. Saffell, “Performance functions and reinforcement learning for trading systems and portfolios,” Journal of forecasting, vol. 17, no. 5-6, pp. 441–470, 1998.
\ [11] S. Sun, M. Qin, H. Xia, C. Zong, J. Ying, Y. Xie, L. Zhao, X. Wang, B. An et al., “Trademaster: A holistic quantitative trading platform empowered by reinforcement learning,” in Thirty-seventh Conference on Neural Information Processing Systems Datasets and Benchmarks Track, 2023.
\ [12] C.-F. Tsai and M.-L. Chen, “Credit rating by hybrid machine learning techniques,” Applied soft computing, vol. 10, no. 2, pp. 374–380, 2010.
\ [13] D. Wang, Z. Chen, I. Florescu, and B. Wen, “A sparsity algorithm for finding optimal counterfactual explanations: Application to corporate credit rating,” Research in International Business and Finance, vol. 64, p. 101869, 2023.
\ [14] Y. Nevmyvaka, Y. Feng, and M. Kearns, “Reinforcement learning for optimized trade execution,” in Proceedings of the 23rd international conference on Machine learning, 2006, pp. 673–680.
\ [15] C. C. Moallemi and M. Wang, “A reinforcement learning approach to optimal execution,” Quantitative Finance, vol. 22, no. 6, pp. 1051–1069, 2022.
\ [16] R. S. Sutton and A. G. Barto, Reinforcement learning: An introduction. MIT press, 2018.
\ [17] A. Coletta, A. Moulin, S. Vyetrenko, and T. Balch, “Learning to simulate realistic limit order book markets from data as a world agent,” in Proceedings of the Third ACM International Conference on AI in Finance, 2022, pp. 428–436.
\ [18] D. Bertsekas, Reinforcement learning and optimal control. Athena Scientific, 2019.
\ [19] V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski et al., “Human-level control through deep reinforcement learning,” nature, vol. 518, no. 7540, pp. 529–533, 2015.
\ [20] J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” arXiv preprint arXiv:1707.06347, 2017.
\ [21] E. Smith, J. D. Farmer, L. Gillemot, and S. Krishnamurthy, “Statistical theory of the continuous double auction,” Quantitative finance, vol. 3, no. 6, p. 481, 2003.
\ [22] T. W Alves, I. Florescu, G. Calhoun, and D. Bozdog, “Shift: A highly realistic financial market simulation platform,” in 6th International Symposium in Computational Economics and Finance, Paris, 2020.
\ [23] E. Ratliff-Crain, C. Van Oort, J. Bagrow, B. Tivnan, and M. Koehler, “Revisiting stylized facts for modern stock markets,” Available at SSRN 4631622, 2023.
\ [24] R. Almgren and N. Chriss, “Optimal execution of portfolio transactions,” Journal of Risk, vol. 3, pp. 5–40, 2001.
\ [25] L. R. Glosten and P. R. Milgrom, “Bid, ask and transaction prices in a specialist market with heterogeneously informed traders,” Journal of financial economics, vol. 14, no. 1, pp. 71–100, 1985.
\ [26] T. E. Copeland and D. Galai, “Information effects on the bid-ask spread,” the Journal of Finance, vol. 38, no. 5, pp. 1457–1469, 1983.
\ [27] B. Putnam, G. McDannel, M. Ayikara, and L. S. Peyyalamitta, “Describing the dynamic nature of transactions costs during political event risk episodes,” High Frequency, vol. 1, no. 1, pp. 6–20, 2018. [Online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/hf2.10018
\ [28] LOBSTER: Limit Order Book System - The Efficient Reconstructor at Humboldt Universitat zu Berlin, Germany http://LOBSTER.wiwi.hu-berlin.de.
\ [29] N. Vadori, L. Ardon, S. Ganesh, T. Spooner, S. Amrouni, J. Vann, M. Xu, Z. Zheng, T. Balch, and M. Veloso, “Towards multi-agent reinforcement learning driven over-the-counter market simulations,” arXiv preprint arXiv:2210.07184, 2022.
\
:::info Authors:
(1) Zhiyuan Yao, Stevens Institute of Technology, Hoboken, New Jersey, USA ([email protected]);
(2) Zheng Li, Stevens Institute of Technology, Hoboken, New Jersey, USA ([email protected]);
(3) Matthew Thomas, Stevens Institute of Technology, Hoboken, New Jersey, USA ([email protected]);
(4) Ionut Florescu, Stevens Institute of Technology, Hoboken, New Jersey, USA ([email protected]).
:::
:::info This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.
:::
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.