This Code Helps You Squeeze More Out of Your GPU for AI Workloads

Github location:

https://github.com/philhopkinsML/CUDA/blob/main/dynamictilesize.cpp

\ Modern GPUs vary in shared memory capacity and computational capabilities. This code dynamically adapts to matrix dimensions and hardware configurations, ensuring maximum efficiency without manual tuning.

\

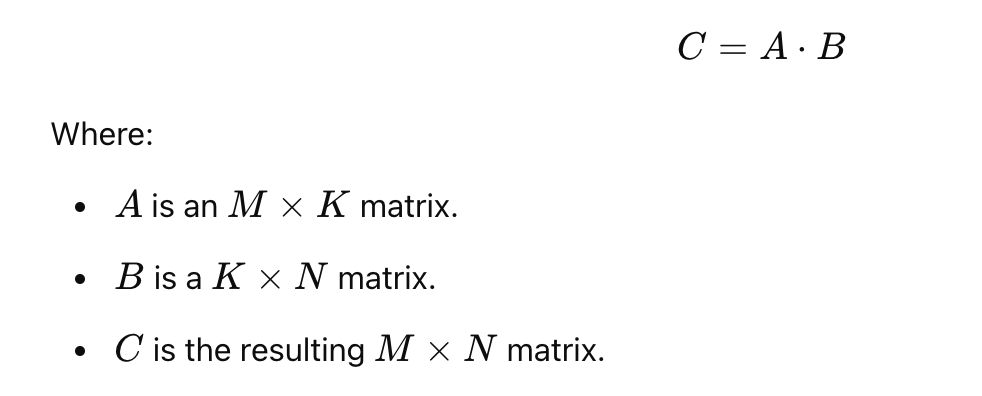
\ \ \ \ \ \ \ \ \ \ It implements a tiled matrix multiplication algorithm, leveraging shared memory on the GPU to minimize the expensive cost of global memory access. Shared memory is faster than global memory but limited in size, so the algorithm dynamically calculates the optimal tile size based on the GPU's properties, ensuring efficient memory utilization.

How It Works Matrix Initialization

The program begins by allocating memory for matrices on both the host (CPU) and device (GPU). These matrices are initialized with example values for demonstration purposes but could easily be replaced with real-world data in practical applications. Here's a relevant snippet:

// Allocate memory for matrices float *h_A, *h_B, *h_C; // Host matrices float *d_A, *d_B, *d_C; // Device matrices int size_A = width * height * sizeof(float); cudaMalloc((void **)&d_A, size_A); cudaMalloc((void **)&d_B, size_B); cudaMalloc((void **)&d_C, size_C); // Initialize matrices with example values initializeMatrix(h_A, width, height); initializeMatrix(h_B, width, height); cudaMemcpy(d_A, h_A, size_A, cudaMemcpyHostToDevice); cudaMemcpy(d_B, h_B, size_B, cudaMemcpyHostToDevice);

This code prepares the matrices for computation by allocating GPU memory and copying data from the host to the device. Efficient data transfer is critical in GPU programming to minimize overhead.

Dynamic Tile Size Calculation

The function DynamicTileSize queries the GPU's properties to determine the optimal tile size. This calculation ensures that:

1. The maximum shared memory per block is respected.
2. The tile size is large enough for efficient computation but small enough to fit within the shared memory constraints.

int DynamicTileSize(int sharedMemPerBlock) { int tileSize = sqrt(sharedMemPerBlock / sizeof(float)); return tileSize; }

This function dynamically calculates the maximum tile size based on the shared memory available on the GPU, ensuring portability across various hardware configurations.

Tiled Matrix Multiplication

The matrixMulTiledDynamic kernel performs matrix multiplication in a block-wise manner using shared memory. Each block processes a submatrix (tile) of the larger matrices. Shared memory is dynamically allocated, reducing the cost of global memory access.

extern __shared__ float sharedMem[]; __global__ void matrixMulTiledDynamic(float *A, float *B, float *C, int N, int tileSize) { int tx = threadIdx.x; int ty = threadIdx.y; float *sharedA = &sharedMem[0]; float *sharedB = &sharedMem[tileSize * tileSize]; float result = 0.0f; for (int m = 0; m < N / tileSize; ++m) { // Load tiles into shared memory sharedA[ty * tileSize + tx] = A[row * N + (m * tileSize + tx)]; sharedB[ty * tileSize + tx] = B[(m * tileSize + ty) * N + col]; __syncthreads(); // Perform multiplication for (int k = 0; k < tileSize; ++k) { result += sharedA[ty * tileSize + k] * sharedB[k * tileSize + tx]; } __syncthreads(); } // Write result to global memory C[row * N + col] = result; }

• Shared Memory: Dynamically allocated and split between submatrices sharedA and sharedB.
• Thread Cooperation: Threads within a block load tiles into shared memory, perform multiplication, and synchronize before writing results back to global memory.
• Dynamic Tile Size: The tileSize parameter, calculated earlier, ensures that shared memory is efficiently utilized.

Challenges Addressed

1. Scalability: The dynamic tile size adapts to larger matrices and more powerful GPUs, ensuring efficient resource usage.
2. Portability: By querying GPU properties (e.g., shared memory per block), the code can run on different GPU architectures without manual tuning.
3. Real-World Usability: Irregular matrix shapes and varying hardware configurations are handled seamlessly.

Real-World Applications

1. Deep Learning: Matrix multiplication is at the core of many deep learning algorithms. This implementation can optimize performance for large-scale computations in training and inference.
2. High-Performance Computing: Scientific simulations often rely on fast and accurate matrix operations, making this code invaluable in fields like physics and engineering.
3. Real-Time Rendering and Transformations: Gaming and real-time applications can use this approach for efficient transformations or physics simulations.

Conclusion

This dynamic tiling approach ensures that matrix multiplication leverages GPU hardware to its fullest potential. By adapting tile sizes based on the GPU's shared memory capabilities, the implementation achieves a balance between scalability, portability, and real-world usability. Whether for deep learning, scientific computing, or real-time applications, this code exemplifies how modern GPUs can handle computationally demanding tasks efficiently and elegantly.

\