A Brief Review of the Lie Group and the Geometries of SPD Manifolds

Abstract and 1 Introduction

2 Preliminaries

3. Revisiting Normalization

3.1 Revisiting Euclidean Normalization

3.2 Revisiting Existing RBN

4 Riemannian Normalization on Lie Groups

5 LieBN on the Lie Groups of SPD Manifolds and 5.1 Deformed Lie Groups of SPD Manifolds

5.2 LieBN on SPD Manifolds

6 Experiments

6.1 Experimental Results

7 Conclusions, Acknowledgments, and References

\ APPENDIX CONTENTS

A Notations

B Basic layes in SPDnet and TSMNet

C Statistical Results of Scaling in the LieBN

D LieBN as a Natural Generalization of Euclidean BN

E Domain-specific Momentum LieBN for EEG Classification

F Backpropagation of Matrix Functions

G Additional Details and Experiments of LieBN on SPD manifolds

H Preliminary Experiments on Rotation Matrices

I Proofs of the Lemmas and Theories in the Main Paper

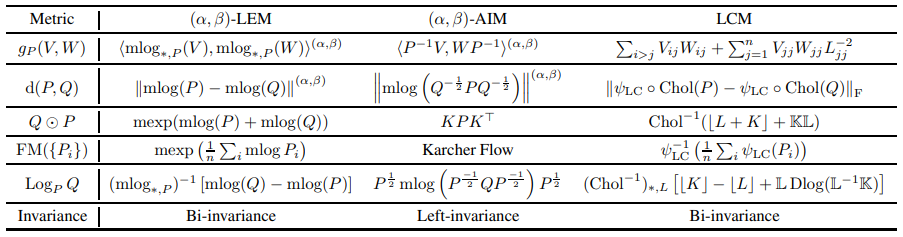
This section provides a brief review of the Lie group and the geometries of SPD manifolds. For more in-depth discussions, please refer to Tu (2011); Do Carmo & Flaherty Francis (1992).

\

\ A Lie group is a group and also a manifold. The most natural Riemannian metric on a Lie group is the left-invariant metric[1]. Similarly, one can define the right-invariant metric as Def. 2.2. A biinvariant Riemannian metric is the one with both left and right invariance. Given the analogous properties of left and right-invariant metrics, this paper focuses on left-invariant metrics.

\ The idea of pullback is ubiquitous in differential geometry and can be considered as a natural counterpart of bijection in the set theory.

\

\

\

\

:::info This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.

:::

[1] Left invariant metric always exists for every Lie group (Do Carmo & Flaherty Francis, 1992).

:::info Authors:

(1) Ziheng Chen, University of Trento;

(2) Yue Song, University of Trento and a Corresponding author;

(3) Yunmei Liu, University of Louisville;

(4) Nicu Sebe, University of Trento.

:::

\