and the distribution of digital products.
ADA Outperforms ERM and Competes with C-Mixup in In-Distribution Generalization Tasks
:::info Authors:
(1) Nora Schneider, Computer Science Department, ETH Zurich, Zurich, Switzerland ([email protected]);
(2) Shirin Goshtasbpour, Computer Science Department, ETH Zurich, Zurich, Switzerland and Swiss Data Science Center, Zurich, Switzerland ([email protected]);
(3) Fernando Perez-Cruz, Computer Science Department, ETH Zurich, Zurich, Switzerland and Swiss Data Science Center, Zurich, Switzerland ([email protected]).
:::
Table of Links2 Background
3.1 Comparison to C-Mixup and 3.2 Preserving nonlinear data structure
4 Experiments and 4.1 Linear synthetic data
4.2 Housing nonlinear regression
4.3 In-distribution Generalization
4.4 Out-of-distribution Robustness
5 Conclusion, Broader Impact, and References
\ A Additional information for Anchor Data Augmentation
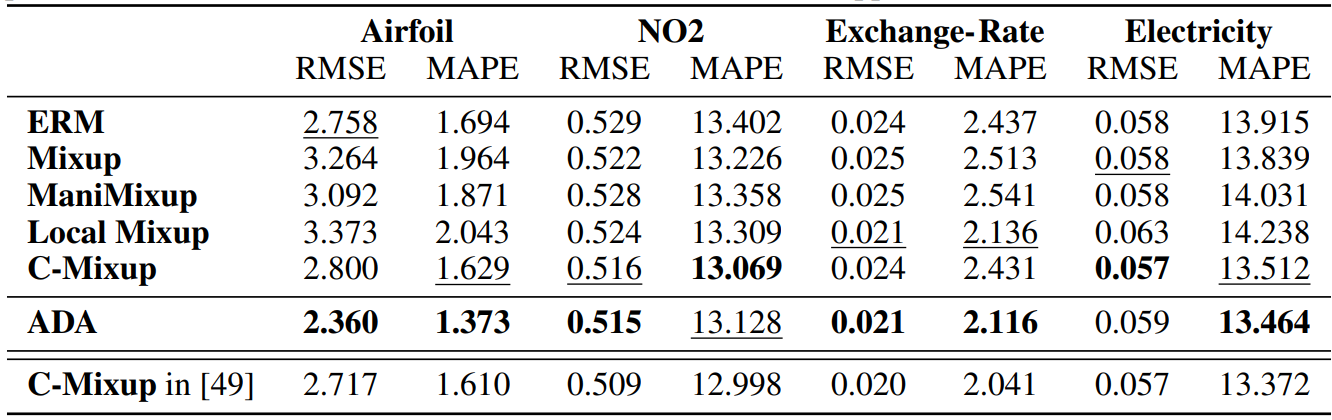
4.3 In-distribution GeneralizationIn this section, we evaluate the performance of ADA and compare it to prior approaches on tasks involving in-distribution generalization. We use the same datasets as [49] and closely follow their experimental setup.
\ Data: We use four of the five in-distribution datasets used in [49]. The validation and test data are expected to follow the same distribution as the training data. Airfoil Self-Noise (Airfoil) and NO2 [24] are both tabular datasets, whereas Exchange-Rate and Electricity [27] are time series datasets. We divide the datasets into train-, validation- and test data randomly, as the authors of C-Mixup did. For Echocardiogram videos [37] (the 5th dataset in [49]), we could not replicate their preprocessing.
\ Models and comparisons: We compare our approach, ADA, to C-Mixup [49], Local-Mixup [2], Manifold-Mixup [46], Mixup [51] and classical expected risk minimization (ERM). Following the work of [49], we use the same model architectures: a three-layer fully connected network for the tabular datasets; and an LST-Attn [27] for the time series.
\ We follow the setup of [49] and apply C-Mixup, Manifold-Mixup, Mixup, and ERM with their reported hyperparameters and provided code. For the ADA and Local-Mixup experiments, we use hyperparameter tuning and grid search to find the optimal training (batch size, learning rate, and number of epochs), and Local-Mixup parameters (distance threshold ϵ) and ADA parameters (number of clusters, range of γ, and whether to use manifold augmentation). We provide a detailed description in Appendix B.4. The evaluation metrics are Root Mean Squared Error (RMSE) and Mean Averaged Percentage Error (MAPE).
\ Results: We report the results in Table 1. For full transparency, in the last row, we copy the results from [49]. We can assess that ADA is competitive with C-Mixup and superior to the other data augmentation strategies. ADA consistently improves the regression fit compared to ERM. Under the same conditions (split of data and Neural network structure), ADA is superior to C-Mixup. But, the degree of improvement is marginal on some datasets and as we show in the last row, we could not fully replicate their results. The only data in which ADA is significantly better than C-Mixup and the other strategies is for the Airfoil data, in which ADA reduces the error by around 15% with respect to the ERM solution.
\
\
:::info This paper is available on arxiv under CC0 1.0 DEED license.
:::
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.