Unveiling Path Signatures: A Key to Geometric Insights in Data

:::info Authors:

(1) Guillaume Staerman, INRIA, CEA, Univ. Paris-Saclay, France;

(2) Marta Campi, CERIAH, Institut de l’Audition, Institut Pasteur, France;

(3) Gareth W. Peters, Department of Statistics & Applied Probability, University of California Santa Barbara, USA.

:::

Abstract and 1. Introduction

2. Background & Preliminaries

2.1. Functional Isolation Forest

2.2. The Signature Method

3. Signature Isolation Forest Method

4. Numerical Experiments

4.1. Parameters Sensitivity Analysis

4.2. Advantages of (K-)SIF over FIF

4.3. Real-data Anomaly Detection Benchmark

5. Discussion & Conclusion, Impact Statements, and References

\ Appendix

A. Additional Information About the Signature

B. K-SIF and SIF Algorithms

C. Additional Numerical Experiments

The signature of a path is a sequence of iterated integrals that captures important information about the path’s geometric and topological features (Lyons et al., 2007; Fermanian, 2021).

\

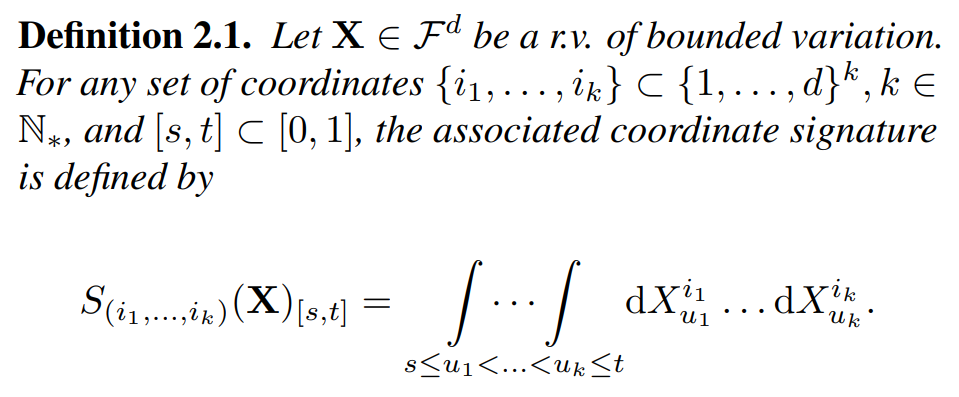
\ Furthermore, the signature of X is defined as the infinite collection of coordinate signature

\

\

\

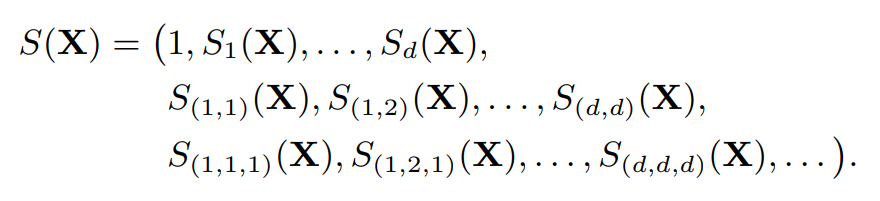
\ One may refer to Lee and Oberhauser (2023) for an account of the untruncated kernel signature. See also Section A in the Appendix for further details about the signature and its properties.

\

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\