and the distribution of digital products.
What Are Gyrocommutative Gyrogroups?
Proposed Approach
C. Formulation of MLR from the Perspective of Distances to Hyperplanes
H. Computation of Canonical Representation
G SOME RELATED DEFINITIONS G.1 GYROGROUPS AND GYROVECTOR SPACESGyrovector spaces form the setting for hyperbolic geometry in the same way that vector spaces form the setting for Euclidean geometry (Ungar, 2002; 2005; 2014). We recap the definitions of gyrogroups and gyrocommutative gyrogroups proposed in Ungar (2002; 2005; 2014). For greater mathematical detail and in-depth discussion, we refer the interested reader to these papers.
\ Definition G.1 (Gyrogroups (Ungar, 2014)). A pair (G, ⊕*) is a groupoid in the sense that it is a nonempty set, G, with a binary operation, ⊕. A groupoid (G,* ⊕*) is a gyrogroup if its binary operation satisfies the following axioms for a, b, c ∈ G:*
\ (G1) There is at least one element e ∈ G called a left identity such that e ⊕ a = a.
\ (G2) There is an element ⊖a ∈ G called a left inverse of a such that ⊖a ⊕ a = e.
\ (G3) There is an automorphism gyr[a, b] : G → G for each a, b ∈ G such that
\ a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ gyr[a, b]c (Left Gyroassociative Law).
\ The automorphism gyr[a, b] is called the gyroautomorphism, or the gyration of G generated by a, b. (G4) gyr[a, b] = gyr[a ⊕ b, b] (Left Reduction Property).
\ Definition G.2 (Gyrocommutative Gyrogroups (Ungar, 2014)). A gyrogroup (G, ⊕*) is gyrocommutative if it satisfies*
\ a ⊕ b = gyr[a, b](b ⊕ a) (Gyrocommutative Law).
\ The following definition of gyrovector spaces is slightly different from Definition 3.2 in Ungar (2014).
\ Definition G.3 (Gyrovector Spaces). A gyrocommutative gyrogroup (G, ⊕) equipped with a scalar multiplication
\ Definition G.3 (Gyrovector Spaces). A gyrocommutative gyrogroup (G, ⊕*) equipped with a scalar multiplication*
\ (t, x) → t ⊙ x : R × G → G
\ is called a gyrovector space if it satisfies the following axioms for s, t ∈ R and a, b, c ∈ G*:*
\ (V1) 1 ⊙ a = a, 0 ⊙ a = t ⊙ e = e, and (−1) ⊙ a = ⊖a.
\ (V2) (s + t) ⊙ a = s ⊙ a ⊕ t ⊙ a.
\ (V3) (st) ⊙ a = s ⊙ (t ⊙ a).
\ (V4) gyr[a, b](t ⊙ c) = t ⊙ gyr[a, b]c.
\ (V5) gyr[s ⊙ a, t ⊙ a] = Id, where Id is the identity map.
G.2 AI GYROVECTOR SPACES
\
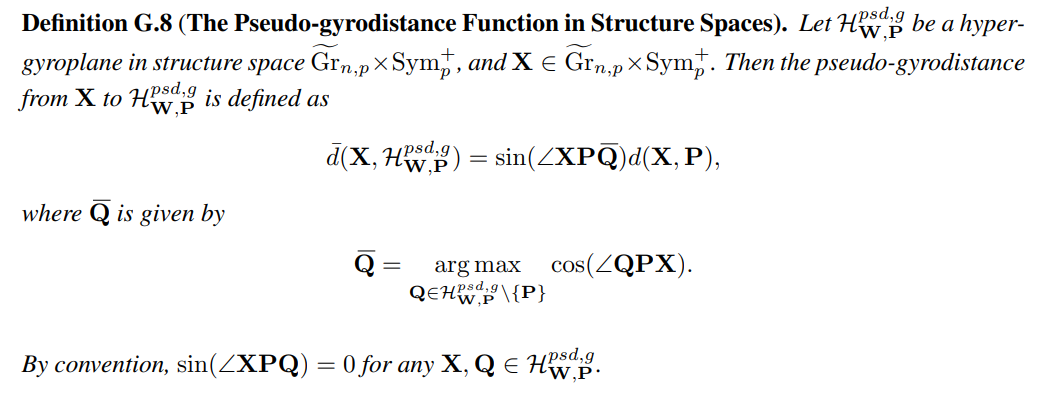
:::info Authors:
(1) Xuan Son Nguyen, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France ([email protected]);
(2) Shuo Yang, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France ([email protected]);
(3) Aymeric Histace, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France ([email protected]).
:::
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\