In this section, we introduce an iterative algorithm for solving the mixed strategy equilibrium system 2.5). As mentioned previously, directly solving system (2.5) is intractable. Instead, we obtain the mixed strategy equilibrium by solving the more tractable pure strategy system (2.4) using fictitious play as follows. First, we introduce a generalized fictitious play and build the convergence result from the pure strategy system to the mixed strategy system through fictitious play for potential games. Next, we present the finite difference schemes used to numerically solve the obstacle and Fokker-Planck equations. Finally, we show the implicit scheme preserves the convergence property from pure to mixed strategies.

3.1 Fictitious Play

Fictitious play is a learning procedure in which, at each step, every agent chooses the best response strategy based on the average of the strategies previously employed by other agents. It would seem natural, therefore, to expect that the best response strategy would converge to the strategy corresponding to the Nash equilibrium of the game. While fictitious play provides a simple approach to approximate the Nash equilibrium, it does not always work. In classical MFG models, it has been proven in [9] that the sequence obtained via fictitious play converges to the MFG solution. When applied to OSMFG models, it has been proven that the linear programming method utilizing fictitious play converges to the relaxed Nash equilibrium under a measure flow framework, as demonstrated in [10]. However, fictitious play has not yet been directly applied to the PDE systems representing the Nash equilibrium for OSMFG models.

\ Our goal is to adapt the fictitious play to the PDE systems in order to find the mixed strategy equilibrium solutions for OSMFG models. The main challenge is to investigate the convergence of the fictitious play of the pure strategy system (2.4) to the solution of the mixed strategy system (2.5). This requires novel theoretical advances since the current results on fictitious play for classic MFG systems analyzed in [9] cannot be applied to OSMFG models, as classic MFG systems do not need the notion of mixed strategy equilibrium.

\ Recall that fictitious play approximates a mixed strategy equilibrium through iterative pure strategies. An agent decides whether to quit the game when using a pure strategy, whereas he specifies the likelihood of quitting the game when using a mixed strategy. This is the main difference between the two notions of equilibrium. In a fictitious play for OSMFG, agents repeatedly play the game, applying a pure strategy that is the best response to the average historic distribution of agents in each instance. Over repeated plays, agents may apply different pure strategies at a given state (x, t). Therefore, at some state (x, t), an agent may quit during some rounds of plays, but for other rounds he may not. Overall, he quits at (x, t) with a probability no less than 0 but no greater than 1. This illustrates the idea behind a mixed strategy.

\ Each iteration of a fictitious play for OSMFG can be divided into the following three steps:

Finding the Best Response. Agents calculate an optimal pure strategy response based on the so-called updated distribution of agents, which encodes the historical information from previous iterations.

\
Propagating the Proposed Distribution. The proposed distribution of agents is determined based on the strategies obtained in the previous step.

\
Calculating the Updated Distribution. The agents calculate the updated distribution by incorporating the proposed distribution with a certain updating rule. The updated distribution will be used to calculate controls in the next iteration.

\ The procedure can be formulated in the definition below.

\ Definition 3.1 (generalized fictitious play) Given the initial distribution m0. The following iteration is called a generalized fictitious play.

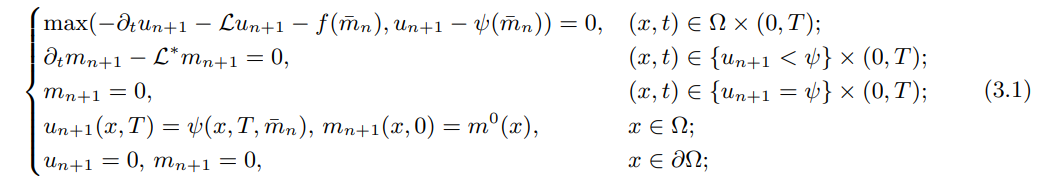
\ where n = 0, 1, 2, … is the iteration round, and

:::info This paper is available on arxiv under CC 4.0 license.

:::

Feed: Hacker Noon - Medium

View: Original article

Tags: distribution framework